
ЁОЬтФПЁПШчЭМЃЌНЋвЛЬѕЪ§жсдкдЕуOКЭЕуBДІИїелвЛЯТЃЌЕУЕНвЛЬѕЁАелЯпЪ§жсЁБЃЎЭМжаЕуAБэЪОЉ11ЃЌЕуBБэЪО10ЃЌЕуCБэЪО18ЃЌЮвУЧГЦЕуAКЭЕуCдкЪ§жсЩЯЯрОр29ИіГЄЖШЕЅЮЛЃЎЖЏЕуPДгЕуAГіЗЂЃЌвд2ЕЅЮЛ/УыЕФЫйЖШбизХЁАелЯпЪ§жсЁБЕФе§ЗНЯђдЫЖЏЃЌДгЕуOдЫЖЏЕНЕуBЦкМфЫйЖШБфЮЊдРДЕФвЛАыЃЌжЎКѓСЂПЬЛжИДдЫйЃЛЭЌЪБЃЌЖЏЕуQДгЕуCГіЗЂЃЌвд1ЕЅЮЛ/УыЕФЫйЖШбизХЪ§жсЕФИКЗНЯђдЫЖЏЃЌДгЕуBдЫЖЏЕНЕуOЦкМфЫйЖШБфЮЊдРДЕФСНБЖЃЌжЎКѓвВСЂПЬЛжИДдЫйЃЎЩшдЫЖЏЕФЪБМфЮЊtУыЃЎ
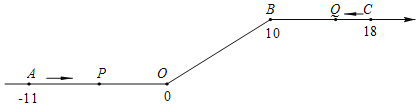
ЮЪЃКЃЈ1ЃЉЖЏЕуPДгЕуAдЫЖЏжСCЕуашвЊЖрЩйЪБМфЃП
ЃЈ2ЃЉPЁЂQСНЕуЯргіЪБЃЌЧѓГіЯргіЕуMЫљЖдгІЕФЪ§ЪЧЖрЩйЃЛ
ЃЈ3ЃЉЧѓЕБtЮЊКЮжЕЪБЃЌPЁЂOСНЕудкЪ§жсЩЯЯрОрЕФГЄЖШгыQЁЂBСНЕудкЪ§жсЩЯЯрОрЕФГЄЖШЯрЕШЃЎ
ЁОД№АИЁПЃЈ1ЃЉ19.5УыЃЛЃЈ2ЃЉMЫљЖдгІЕФЪ§ЮЊ5ЃЛЃЈ3ЃЉtЕФжЕЮЊ3ЁЂ6.75ЁЂ10.5Лђ18
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнТЗГЬГ§вдЫйЖШЕШгкЪБМфЃЌПЩЕУД№АИЃЛ
ЃЈ2ЃЉИљОнЯргіЪБPЃЌQЕФЪБМфЯрЕШЃЌПЩЕУЗНГЬЃЌИљОнНтЗНГЬЃЌПЩЕУД№АИЃЛ
ЃЈ3ЃЉИљОнPOгыBQЕФЪБМфЯрЕШЃЌПЩЕУЗНГЬЃЌИљОнНтЗНГЬЃЌПЩЕУД№АИЃЎ
НтЃКЃЈ1ЃЉЕуPдЫЖЏжСЕуCЪБЃЌЫљашЪБМфtЃН11ЁТ2+10ЁТ1+8ЁТ2ЃН19.5ЃЈУыЃЉЃЌ
Д№ЃКЖЏЕуPДгЕуAдЫЖЏжСCЕуашвЊ19.5ЪБМфЃЛ
ЃЈ2ЃЉгЩЬтПЩжЊЃЌPЁЂQСНЕуЯргідкЯпЖЮOBЩЯгкMДІЃЌЩшOMЃНxЃЎ
дђ11ЁТ2+xЁТ1ЃН8ЁТ1+ЃЈ10ЉxЃЉЁТ2ЃЌ
xЃН5ЃЌ
Д№ЃКMЫљЖдгІЕФЪ§ЮЊ5ЃЎ
ЃЈ3ЃЉPЁЂOСНЕудкЪ§жсЩЯЯрОрЕФГЄЖШгыQЁЂBСНЕудкЪ§жсЩЯЯрОрЕФГЄЖШЯрЕШга4жжПЩФмЃК
ЂйЖЏЕуQдкCBЩЯЃЌЖЏЕуPдкAOЩЯЃЌ
дђЃК8ЉtЃН11Љ2tЃЌНтЕУЃКtЃН3ЃЎ
ЂкЖЏЕуQдкCBЩЯЃЌЖЏЕуPдкOBЩЯЃЌ
дђЃК8ЉtЃНЃЈtЉ5.5ЃЉЁС1ЃЌНтЕУЃКtЃН6.75ЃЎ
ЂлЖЏЕуQдкBOЩЯЃЌЖЏЕуPдкOBЩЯЃЌ
дђЃК2ЃЈtЉ8ЃЉЃНЃЈtЉ5.5ЃЉЁС1ЃЌНтЕУЃКtЃН10.5ЃЎ
ЂмЖЏЕуQдкOAЩЯЃЌЖЏЕуPдкBCЩЯЃЌ
дђЃК10+2ЃЈtЉ15.5ЃЉЃНtЉ13+10ЃЌНтЕУЃКtЃН18ЃЌ
злЩЯЫљЪіЃКtЕФжЕЮЊ3ЁЂ6.75ЁЂ10.5Лђ18ЃЎ


 Ек1ОэЕЅдЊдТПМЦкжаЦкФЉЯЕСаД№АИ
Ек1ОэЕЅдЊдТПМЦкжаЦкФЉЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
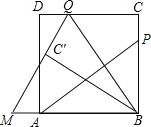
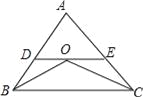
ЁОЬтФПЁПШчЭМЃЌPЮЊе§ЗНаЮABCDЕФБпBCЩЯвЛЖЏЕу(PгыBЁЂCВЛжиКЯ)ЃЌСЌНгAPЃЌЙ§ЕуBзїBQЁЭAPНЛCDгкЕуQЃЌНЋЁїBQCбиBQЫљдкЕФжБЯпЖделЕУЕНЁїBQCЁфЃЌбгГЄQCЁфНЛBAЕФбгГЄЯпгкЕуMЃЎ
(1)ЪдЬНОПAPгыBQЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
(2)ЕБAB=3ЃЌBP=2PCЃЌЧѓQMЕФГЄЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
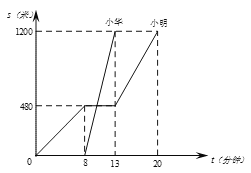
ЁОЬтФПЁПаЁУїКЭаЁЛЊЪЧЭЌАрЭЌбЇЃЌвВЪЧСкОгЃЌФГШедчГПЃЌаЁУї7ЃК40ЯШГіЗЂШЅбЇаЃЃЌзпСЫвЛЖЮКѓЃЌдкЭОжаЭЃЯТГдСЫдчВЭЃЌКѓРДЗЂЯжЩЯбЇЪБМфПьЕНСЫЃЌОЭХмВНЕНбЇаЃЃЛаЁЛЊРыМвКѓжБНгГЫЙЋЙВЦћГЕЕНСЫбЇаЃЃЎШчЭМЪЧЫћУЧДгМвЕНбЇаЃвбзпЕФТЗГЬsЃЈУзЃЉКЭЫљгУЪБМфtЃЈЗжжгЃЉЕФЙиЯЕЭМЃЎдђЯТСаЫЕЗЈжа
ЂйаЁУїМвгыбЇаЃЕФОрРы1200УзЃЛ
ЂкаЁЛЊГЫзјЙЋЙВЦћГЕЕФЫйЖШЪЧ240Уз/ЗжЃЛ
ЂлаЁЛЊГЫзјЙЋЙВЦћГЕКѓ7:50гыаЁУїЯргіЃЛ
ЂмаЁЛЊЕФГіЗЂЪБМфВЛБфЃЌЕБаЁЛЊгЩГЫЙЋЙВЦћГЕБфЮЊХмВНЃЌЧвХмВНЕФЫйЖШЪЧ100Уз/ЗжЪБЃЌЫћУЧПЩвдЭЌЪБЕНДябЇаЃ.Цфжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
A. 1 ИіB. 2Иі
C. 3 ИіD. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэИјГіСЫДњЪ§ЪНЉx2+bx+cгыxЕФвЛаЉЖдгІжЕЃК
x | Ё | Љ2 | Љ1 | 0 | 1 | 2 | 3 | Ё |
Љx2+bx+c | Ё | 5 | n | c | 2 | Љ3 | Љ10 | Ё |
ЃЈ1ЃЉИљОнБэИёжаЕФЪ§ОнЃЌШЗЖЈbЃЌcЃЌnЕФжЕЃЛ
ЃЈ2ЃЉЩшy=Љx2+bx+cЃЌжБНгаДГі0ЁмxЁм2ЪБyЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
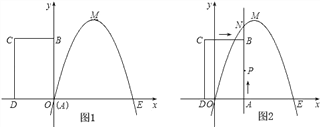
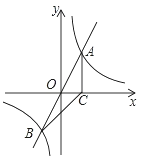
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпОЙ§зјБъдЕуOКЭxжсЩЯСэвЛЕуEЃЌЖЅЕуMЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЛОиаЮABCDЕФЖЅЕуAгыЕуOжиКЯЃЌADЁЂABЗжБ№дкxжсЁЂyжсЩЯЃЌЧвAD=2ЃЌAB=3ЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉНЋОиаЮABCDвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгШчЭМЫљЪОЕФЮЛжУбиxжсЕФе§ЗНЯђдШЫйЦНаавЦЖЏЃЌЭЌЪБвЛЖЏЕуPвВвдЯрЭЌЕФЫйЖШДгЕуAГіЗЂЯђBдШЫйвЦЖЏЃЌЩшЫќУЧдЫЖЏЕФЪБМфЮЊtУыЃЈ0ЁмtЁм3ЃЉЃЌжБЯпABгыИУХзЮяЯпЕФНЛЕуЮЊNЃЈШчЭМ2ЫљЪОЃЉЃЎ
ЂйЕБt=![]() ЪБЃЌХаЖЯЕуPЪЧЗёдкжБЯпMEЩЯЃЌВЂЫЕУїРэгЩЃЛ
ЪБЃЌХаЖЯЕуPЪЧЗёдкжБЯпMEЩЯЃЌВЂЫЕУїРэгЩЃЛ
ЂкЩшвдPЁЂNЁЂCЁЂDЮЊЖЅЕуЕФЖрБпаЮУцЛ§ЮЊSЃЌЪдЮЪSЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧѓГіетИізюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєИЩИіЙЄШЫзАаЖвЛХњЛѕЮяЃЌУПИіЙЄШЫЕФзАаЖЫйЖШЯрЭЌЃЌШчЙћетаЉЙЄШЫЭЌЪБЙЄзїЃЌдђаш10аЁЪБзАаЖЭъБЯЃЛЯжИФБфзАаЖЗНЪНЃЌПЊЪМвЛИіШЫИЩЃЌвдКѓУПИєtЃЈећЪ§ЃЉаЁЪБдіМгвЛИіШЫИЩЃЌУПИіВЮМгзАаЖЕФШЫЖМвЛжБИЩЕНзАаЖЭъБЯЃЌЧвзюКѓВЮМгЕФвЛИіШЫзАаЖЕФЪБМфЪЧЕквЛИіШЫЕФ![]() ЃЌдђАДИФБфЕФЗНЪНзАаЖЃЌздЪМжСжеЙВашЪБМф_____аЁЪБЃЎ
ЃЌдђАДИФБфЕФЗНЪНзАаЖЃЌздЪМжСжеЙВашЪБМф_____аЁЪБЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЁїABCжаЃЌBOЃЌCOЗжБ№ЪЧЁЯABCКЭЁЯACBЕФЦНЗжЯпЃЌЙ§OЕуЕФжБЯпЗжБ№НЛABЁЂACгкЕуDЁЂEЃЌЧвDEЁЮBCЃЎШєAB=6 cmЃЌAC=8 cmЃЌдђЁїADEЕФжмГЄЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМУФЯФГжабЇдкВЮМгЁАДДЮФУїГЧЃЌЕудоШЊГЧЁБЪщЛБШШќжаЃЌбюРЯЪІДгШЋаЃ30ИіАржаЫцЛњГщШЁСЫ4ИіАрЃЈгУAЃЌBЃЌCЃЌDБэЪОЃЉЃЌЖдеїМЏЕНЕФзїЖІЕФЪ§СПНјааСЫЗжЮіЭГМЦЃЌжЦзїСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЎ

ЧыИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈlЃЉбюРЯЪІВЩгУЕФЕїВщЗНЪНЪЧЁЁ ЁЁЃЈЬюЁАЦеВщЁБЛђЁАГщбљЕїВщЁБЃЉЃЛ
ЃЈ2ЃЉЧыВЙГфЭъећЬѕаЮЭГМЦЭМЃЌВЂМЦЫуЩШаЮЭГМЦЭМжаCАрзїЦЗЪ§СПЫљЖдгІЕФдВаФНЧЖШЪ§ЁЁ ЁЁЃЎ
ЃЈ3ЃЉЧыЙРМЦШЋаЃЙВеїМЏзїЦЗЕФЪВЪ§ЃЎ
ЃЈ4ЃЉШчЙћШЋжІеїМЏЕФзїЦЗжага5МўЛёЕУвЛЕШНБЃЌЦфжага3УћзїепЪЧФаЩњЃЌ2УћзїепЪЧХЎЩњЃЌЯжвЊдкЛёЕУвЛбљЕШНБЕФзїепжабЁШЁСНШЫВЮМгБэеУзљЬИЛсЃЌЧыФугУСаБэЛђЪїзДЭМЕФЗНЗЈЃЌЧѓЧЁКУбЁШЁЕФСНУћбЇЩњадБ№ЯрЭЌЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§БШР§КЏЪ§![]() ЕФЭМЯёгыЗДБШР§КЏЪ§
ЕФЭМЯёгыЗДБШР§КЏЪ§![]() ЕФЭМЯёНЛгк
ЕФЭМЯёНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЙ§Еу
СНЕуЃЌЙ§Еу![]() зї
зї![]() ДЙжБ
ДЙжБ![]() жсгкЕу
жсгкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() .Шє
.Шє![]() ЕФУцЛ§ЮЊ2.
ЕФУцЛ§ЮЊ2.
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉжБНгаДГіЃКЂйЕу![]() зјБъ____________ЃЛЕу
зјБъ____________ЃЛЕу![]() зјБъ_____________ЃЛЂкЕБ
зјБъ_____________ЃЛЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇ__________________ЃЛ
ЕФШЁжЕЗЖЮЇ__________________ЃЛ
ЃЈ3ЃЉ![]() жсЩЯЪЧЗёДцдквЛЕу
жсЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕу
ЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com