
【题目】如图,CE是ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四边形AFOE:S△COD=2:3.
其中正确的结论有_____.(填写所有正确结论的序号)
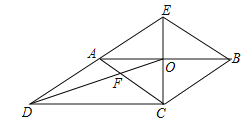
【答案】①②④.
【解析】
根据菱形的判定方法、平行线分线段成比例定理、直角三角形斜边中线的性质一一判断即可.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵EC垂直平分AB,
∴OA=OB=![]() AB=
AB=![]() DC,CD⊥CE,
DC,CD⊥CE,
∵OA∥DC,
∴![]() =
=![]() ,
,
∴AE=AD,OE=OC,
∵OA=OB,OE=OC,
∴四边形ACBE是平行四边形,
∵AB⊥EC,
∴四边形ACBE是菱形,故①正确,
∵∠DCE=90°,DA=AE,
∴AC=AD=AE,
∴∠ACD=∠ADC=∠BAE,故②正确,
∵OA∥CD,
∴![]() ,
,
∴![]() ,故③错误,
,故③错误,
设△AOF的面积为a,则△OFC的面积为2a,△CDF的面积为4a,△AOC的面积=△AOE的面积=3a,
∴四边形AFOE的面积为4a,△ODC的面积为6a
∴S四边形AFOE:S△COD=2:3.故④正确.
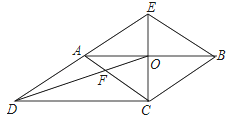
故答案是:①②④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于河南省郑州市的炎黄二帝巨型塑像,是为代表中华民族之创始、之和谐、之统一.塑像由山体CD和头像AD两部分组成.某数学兴趣小组在塑像前50米处的B处测得山体D处的仰角为45°,头像A处的仰角为70.5°,求头像AD的高度.(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
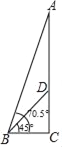
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,
(1)BC= m,AC= m;
(2)现在计划在斜坡AB的中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE,若斜坡BE的坡角为30°,求平台DE的长;(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
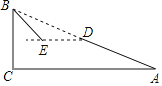
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+mx﹣2m﹣4(m>0).
(1)证明:该抛物线与x轴总有两个不同的交点;
(2)设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.
①试判断:不论m取任何正数,⊙P是否经过y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;
②若点C关于直线x![]() 的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求
的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB为⊙O的直径,点C,E在⊙O上,![]() ,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F.
,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F.
(1)求证:CF=BF;
(2)若cos∠ABE![]() ,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.
,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是![]()
![]()
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,P是直线AC上一点,AD⊥BP于D,以AD为边作等边△ADE(D,E在直线AC异侧).
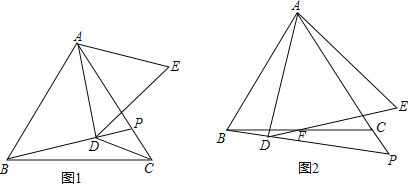
(1)如图1,若点P在边AC上,连CD,且∠BDC=150°,则![]() = ;(直接写结果)
= ;(直接写结果)
(2)如图2,若点P在AC延长线上,DE交BC于F求证:BF=CF;
(3)在图2中,若∠PBC=15°,AB=![]() ,请直接写出CP的长 .
,请直接写出CP的长 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com