
【题目】已知△ABC为等边三角形,P是直线AC上一点,AD⊥BP于D,以AD为边作等边△ADE(D,E在直线AC异侧).
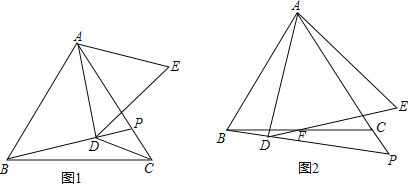
(1)如图1,若点P在边AC上,连CD,且∠BDC=150°,则![]() = ;(直接写结果)
= ;(直接写结果)
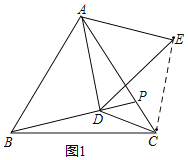
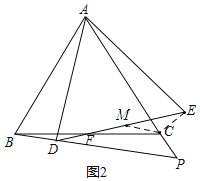
(2)如图2,若点P在AC延长线上,DE交BC于F求证:BF=CF;
(3)在图2中,若∠PBC=15°,AB=![]() ,请直接写出CP的长 .
,请直接写出CP的长 .
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
(1)由题意可证△ABD≌△ACE,可得BD=CE,∠ABD=∠ACE,即可求∠EDC=60°,∠EDC=90°,则可得![]() 的值;
的值;
(2)过点CM∥BD交DE于点M,连接CE,由题意可证△ABD≌△ACE,可得BD=CE,∠AEC=∠ADB=90°,可求∠DEC=∠EMC=30°,可得MC=EC=BD,
则可证△BDF≌△CMF,可得BF=CF;
(3)作∠ABG=∠BAD,交AD于点G,由题意可求∠ABG=∠BAG=15°,可得∠BGD=30°,BG=AG,则可得BG=2BD,GD=![]() BD,AD=
BD,AD=![]() BD+2BD,根据勾股定理可求BD=1,AD=2+
BD+2BD,根据勾股定理可求BD=1,AD=2+![]() ,即可求AP的长,则可求CP的长.
,即可求AP的长,则可求CP的长.
(1)如图:连接CE
∵△ABC,△ADE是等边三角形,
∴AB=AC,AD=AE,∠DAE=∠BAC=60°,
∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ADB=90°,∠BDC=150°,∠ADE=60°,
∴∠EDC=60°,
∵∠BDC=∠BPC+∠ACD=∠BAC+∠ABD+∠ACD=60°+∠ACE+∠ACD=60°+∠ECD=150°
∴∠ECD=90°,
∴tan∠EDC=![]() ,
,
∴![]() ;
;
(2)如图:过点CM∥BD交DE于点M,连接CE
∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°=∠ADE=∠AED,
∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△ABD≌△ACE(ASA),
∴BD=CE,∠AEC=∠ADB=90°,
∵∠BDE=∠ADB+∠ADE,∠DEC=∠AEC-∠AED,
∴∠BDE=150°,∠DEC=30°,
∵MC∥BD,
∴∠DMC=∠BDE=150°,
∴∠EMC=30°,
∴∠DEC=∠EMC,
∴MC=CE,
∴BD=CM,且∠BDE=∠CMD,∠BFD=∠CFM,
∴△BDF≌△CMF(AAS),
∴CF=BF,
(3)如图:作∠ABG=∠BAD,交AD于点G
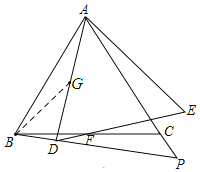
∵∠ABC=60°,∠PBC=15°,AD⊥BD,
∴∠DAB=15°,
∵∠ABG=∠BAD,
∴∠ABG=∠BAG=15°,
∴∠BGD=30°,BG=AG,
∴BG=2BD,GD=![]() BD,
BD,
∴AD=![]() BD+2BD,
BD+2BD,
在Rt△ABD中,AB2=BD2+AD2.
∴(![]() +
+![]() )2=(
)2=(![]() +2)2 BD2+BD2.
+2)2 BD2+BD2.
∴BD=1,
∴AD=2+![]() ,
,
∵∠BAD=15°,∠BAC=60°,
∴∠DAP=45°,且AD⊥BD,
∴AP=![]() AD=2
AD=2![]() +
+![]() ,
,
∵CP=AP-AC=AP-AB=2![]() +
+![]() -(
-(![]() +
+![]() ),
),
∴CP=![]() .
.
故答案为![]() .
.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线![]() 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).
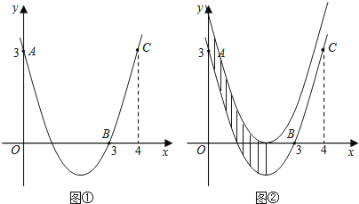
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
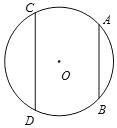
【题目】如图,直径为 10cm 的⊙O 中,两条弦 AB,CD 分别位于圆心的异侧,AB∥CD,且![]() ,若 AB=8cm,则 CD 的长为_____cm.
,若 AB=8cm,则 CD 的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
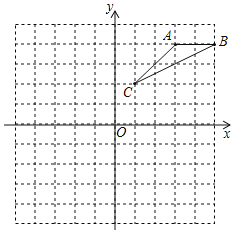
【题目】如图,在平面直角坐标系中,![]() 的三个顶点都在格点上,点A的坐标为
的三个顶点都在格点上,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,请解答下列问题:
,请解答下列问题:
![]() 画出
画出![]() 关于y轴对称的
关于y轴对称的![]() ,使点
,使点![]() 与A对应,点
与A对应,点![]() 与B对应;
与B对应;
![]() 画出
画出![]() 绕原点O顺时针旋转
绕原点O顺时针旋转![]() 后得到的
后得到的![]() ,使点
,使点![]() 与A对应,点
与A对应,点![]() 与B对应;
与B对应;
![]() 若
若![]() 和
和![]() 关于某直线对称,请直接写出该直线的解析式______;
关于某直线对称,请直接写出该直线的解析式______;
![]() 直接写出
直接写出![]() 外接圆圆心的坐标______
外接圆圆心的坐标______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)4(x-1)2=100
(2)x2-2x-15=0
(3)3x2-13x-10=0
(4)3(x-3)2+x(x-3)=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片分别沿两条不同的直线剪两刀,可以使剪得的三块纸片恰能拼成一个等腰三角形(不能有重叠和缝隙).小华的做法是:如图1所示,在矩形ABCD中,分别取AD、AB、CD的中点P、E、F,并沿直线PE 、PF剪两刀,所得的三部分可拼成等腰三角形△PMN (如图2).
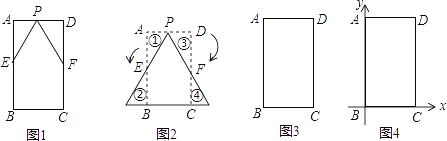
(1)在图3中画出另一种剪拼成等腰三角形的示意图;
(2)以矩形ABCD的顶点B为原点,BC所在直线为x轴建立平面直角坐标系(如图4),矩形ABCD剪拼后得到等腰三角形△PMN,点P在边AD上(不与点A、D重合),点M、N在x轴上(点M在N的左边).如果点D的坐标为(5,8),直线PM的解析式为y=kx+b,求所有满足条件的k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
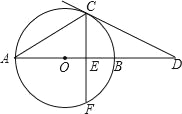
【题目】如图,AB为⊙O的直径,弦CF⊥AB于点E,CF=4![]() ,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 所在的直线上运动,作
所在的直线上运动,作![]() (
(![]() 、
、![]() 、
、![]() 按逆时针方向).
按逆时针方向).
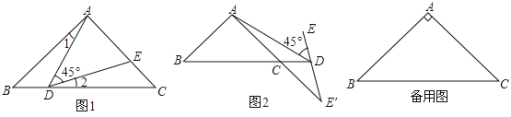
(1)如图①,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 交
交![]() 于
于![]() .
.
①求证:![]() .
.
②当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.
(2)如图②,当点![]() 在
在![]() 的延长线上运动,
的延长线上运动,![]() 的反向延长线与
的反向延长线与![]() 的延长线相交于点
的延长线相交于点![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,写出点
是等腰三角形?若存在,写出点![]() 的位置;若不存在,请简要说明理由.
的位置;若不存在,请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com