
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)由已知角相等,利用对顶角相等,等量代换得到同位角相等,进而得出DB与EC平行,再由内错角相等两直线平行得到DE与BC平行,即可得证;
(2)由角平分线得到一对角相等,再由两直线平行内错角相等,等量代换得到一对角相等,再利用等角对等边得到CN=BC,再由平行四边形对边相等即可确定出所求.
(1)证明:∵∠A=∠F,
∴DE∥BC,
∵∠1=∠2,且∠1=∠DMF,
∴∠DMF=∠2,
∴DB∥EC,
则四边形BCED为平行四边形;
(2)解:∵BN平分∠DBC,
∴∠DBN=∠CBN,
∵EC∥DB,
∴∠CNB=∠DBN,
∴∠CNB=∠CBN,
∴CN=BC=DE=2.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在五边形ABCDE中,AB=AC=AD=AE, 且AB∥ED,∠AED=70°,则∠DCB=( )
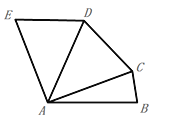
A. 70° B. 165° C. 155° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【回顾】
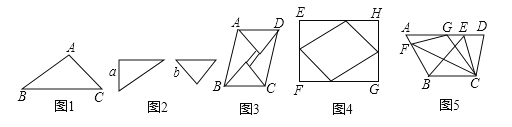
如图1,△ABC中,∠B=30°,AB=3,BC=4,则△ABC的面积等于 .
【探究】
图2是同学们熟悉的一副三角尺,一个含有30°的角,较短的直角边长为a;另一个含有45°的角,直角边长为b,小明用两副这样的三角尺拼成一个平行四边形ABCD(如图3),用了两种不同的方法计算它的面积,从而推出sin75°=![]() ,小丽用两副这样的三角尺拼成了一个矩形EFGH(如图4),也推出sin75°=
,小丽用两副这样的三角尺拼成了一个矩形EFGH(如图4),也推出sin75°=![]() ,请你写出小明或小丽推出sin75°=
,请你写出小明或小丽推出sin75°=![]() 的具体说理过程.
的具体说理过程.
【应用】
在四边形ABCD中,AD∥BC,∠D=75°,BC=6,CD=5,AD=10(如图5).
(1)点E在AD上,设t=BE+CE,求t2的最小值;
(2)点F在AB上,将△BCF沿CF翻折,点B落在AD上的点G处,点G是AD的中点吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF、ON交于点B、点C,连接AB、PB.
(1)如图1,当P、Q两点都在射线ON上时,请直接写出线段AB与PB的数量关系;
(2)如图2,当P、Q两点都在射线ON的反向延长线上时,线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
(3)如图3,∠MON=60°,连接AP,设![]() =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O.
(1)若∠EOF=54°,求∠AOC的度数;
(2)①在∠AOD的内部作射线OG⊥OE;
②试探索∠AOG与∠EOF之间有怎样的关系?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com