
ЁОЬтФПЁПЁОЛиЙЫЁП
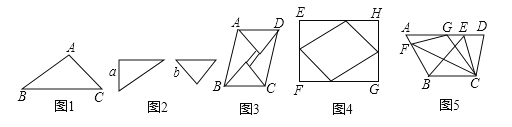
ШчЭМ1ЃЌЁїABCжаЃЌЁЯB=30ЁуЃЌAB=3ЃЌBC=4ЃЌдђЁїABCЕФУцЛ§ЕШгк ЃЎ
ЁОЬНОПЁП
ЭМ2ЪЧЭЌбЇУЧЪьЯЄЕФвЛИБШ§НЧГпЃЌвЛИіКЌга30ЁуЕФНЧЃЌНЯЖЬЕФжБНЧБпГЄЮЊaЃЛСэвЛИіКЌга45ЁуЕФНЧЃЌжБНЧБпГЄЮЊbЃЌаЁУїгУСНИБетбљЕФШ§НЧГпЦДГЩвЛИіЦНааЫФБпаЮABCDЃЈШчЭМ3ЃЉЃЌгУСЫСНжжВЛЭЌЕФЗНЗЈМЦЫуЫќЕФУцЛ§ЃЌДгЖјЭЦГіsin75Ёу=![]() ЃЌаЁРігУСНИБетбљЕФШ§НЧГпЦДГЩСЫвЛИіОиаЮEFGHЃЈШчЭМ4ЃЉЃЌвВЭЦГіsin75Ёу=
ЃЌаЁРігУСНИБетбљЕФШ§НЧГпЦДГЩСЫвЛИіОиаЮEFGHЃЈШчЭМ4ЃЉЃЌвВЭЦГіsin75Ёу=![]() ЃЌЧыФуаДГіаЁУїЛђаЁРіЭЦГіsin75Ёу=
ЃЌЧыФуаДГіаЁУїЛђаЁРіЭЦГіsin75Ёу=![]() ЕФОпЬхЫЕРэЙ§ГЬЃЎ
ЕФОпЬхЫЕРэЙ§ГЬЃЎ
ЁОгІгУЁП
дкЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯD=75ЁуЃЌBC=6ЃЌCD=5ЃЌAD=10ЃЈШчЭМ5ЃЉЃЎ
ЃЈ1ЃЉЕуEдкADЩЯЃЌЩшt=BE+CEЃЌЧѓt2ЕФзюаЁжЕЃЛ
ЃЈ2ЃЉЕуFдкABЩЯЃЌНЋЁїBCFбиCFЗелЃЌЕуBТфдкADЩЯЕФЕуGДІЃЌЕуGЪЧADЕФжаЕуТ№ЃПЫЕУїРэгЩЃЎ
ЁОД№АИЁПЁОЛиЙЫЁП3ЃЛЁОЬНОПЁПД№АИМћНтЮіЃЛЁОгІгУЁПЃЈ1ЃЉ86+25![]() ЃЛЃЈ2ЃЉЕуGВЛЪЧADЕФжаЕуЃЎ
ЃЛЃЈ2ЃЉЕуGВЛЪЧADЕФжаЕуЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЛиЙЫЃКШчЭМ1жаЃЌзїAHЁЭBCЃЎЧѓГіAHМДПЩНтОіЮЪЬтЃЛ
ЬНОПЃКШчЭМ2жаЃЌИљОнSЫФБпаЮABCD=BCABsin75Ёу=2SЁїABE+2SЁїBFC+SОиаЮEFGHСаГіЗНГЬМДПЩНтОіЮЪЬтЃЛ
гІгУЃКЃЈ1ЃЉзїCЙигкADЕФЖдГЦЕуHЃЌCHНЛADгкJЃЌСЌНгBHЃЌEHЃЎвђЮЊEC=EHЃЌЭЦГіEB+EC=EB+EHЃЌдкЁїEBHжаЃЌBE+EHЁнBHЃЌЭЦГіBE+ECЕФзюаЁжЕЮЊBHЃЌЧѓГіBHМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉНсТлЃКЕуGВЛЪЧADЕФжаЕуЃЎРэгЩЗДжЄЗЈжЄУїМДПЩЃЎ
ЪдЬтНтЮіЃКНтЃКгЩЬтвтПЩжЊЫФБпаЮEFGHЪЧОиаЮЃЌAB=CD=2aЃЌAH=DH=BF=CF=bЃЌEF=GH=![]() aЉbЃЌEH=FG=bЉaЃЌBC=
aЉbЃЌEH=FG=bЉaЃЌBC=![]() bЃЎ
bЃЎ
ЁОЛиЙЫЁПШчЭМ1жаЃЌзїAHЁЭBCЃЎ
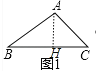
дкRtЁїABHжаЃЌЁпЁЯB=30ЁуЃЌAB=3ЃЌЁрAH=ABsin30Ёу=![]() ЃЌЁрSЁїABC=
ЃЌЁрSЁїABC=![]() BCAH=
BCAH=![]() ЁС4ЁС
ЁС4ЁС![]() =3ЃЌЙЪД№АИЮЊЃК3ЃЎ
=3ЃЌЙЪД№АИЮЊЃК3ЃЎ
ЬНОПЃКШчЭМ3жаЃЌ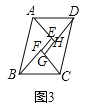
гЩЬтвтПЩжЊЫФБпаЮEFGHЪЧОиаЮЃЌAB=CD=2aЃЌAH=DH=BF=CF=bЃЌEF=GH=![]() aЉbЃЌEH=FG=bЉaЃЌBC=
aЉbЃЌEH=FG=bЉaЃЌBC=![]() bЃЌЁпSЫФБпаЮABCD=BCABsin75Ёу=2SЁїABE+2SЁїBFC+SОиаЮEFGH
bЃЌЁпSЫФБпаЮABCD=BCABsin75Ёу=2SЁїABE+2SЁїBFC+SОиаЮEFGH
Ёр![]() b2asin75Ёу=2ЁС
b2asin75Ёу=2ЁС![]() ЁСaЁС
ЁСaЁС![]() a+2ЁС
a+2ЁС![]() ЁСb2+ЃЈ
ЁСb2+ЃЈ![]() aЉbЃЉЃЈbЉaЃЉЃЌЁр2
aЉbЃЉЃЈbЉaЃЉЃЌЁр2![]() absin75Ёу=
absin75Ёу=![]() ab+abЃЌЁрsin75Ёу=
ab+abЃЌЁрsin75Ёу=![]() ЃЎ
ЃЎ
ШчЭМ4жаЃЌ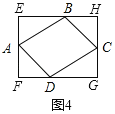
взжЊЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌЁЯBAD=75ЁуЃЌЁрSЫФБпаЮEFGH=2SЁїABE+2SЁїADF+SЦНааЫФБпаЮABCDЃЌЁрЃЈa+bЃЉЃЈ![]() a+bЃЉЈT2ЁС
a+bЃЉЈT2ЁС![]() ЁСaЁС
ЁСaЁС![]() a+2ЁС
a+2ЁС![]() ЁСb2+
ЁСb2+![]() b2asin75ЁуЃЌЁрsin75Ёу=
b2asin75ЁуЃЌЁрsin75Ёу=![]() ЃЎ
ЃЎ
гІгУЃКЃЈ1ЃЉзїCЙигкADЕФЖдГЦЕуHЃЌCHНЛADгкJЃЌСЌНгBHЃЌEHЃЎ
дкRtЁїDCJжаЃЌJC=CDsin75Ёу=![]() ЃЌЁрCH=2CJ=
ЃЌЁрCH=2CJ=![]() ЃЌдкRtЁїBHCжаЃЌBH2=BC2+CH2=36+
ЃЌдкRtЁїBHCжаЃЌBH2=BC2+CH2=36+![]() =86+25
=86+25![]() ЃЌЁпEC=EHЃЌЁрEB+EC=EB+EHЃЌдкЁїEBHжаЃЌBE+EHЁнBHЃЌЁрBE+ECЕФзюаЁжЕЮЊBHЃЌЁрt=BE+CEЃЌt2ЕФзюаЁжЕЮЊBH2ЃЌМДЮЊ86+25
ЃЌЁпEC=EHЃЌЁрEB+EC=EB+EHЃЌдкЁїEBHжаЃЌBE+EHЁнBHЃЌЁрBE+ECЕФзюаЁжЕЮЊBHЃЌЁрt=BE+CEЃЌt2ЕФзюаЁжЕЮЊBH2ЃЌМДЮЊ86+25![]() ЃЎ
ЃЎ
ЃЈ2ЃЉНсТлЃКЕуGВЛЪЧADЕФжаЕуЃЎ
РэгЩЃКзїCJЁЭADгкJЃЌDHЁЭCGгкHЃЎ
ВЛЗСЩшAG=GD=5ЃЌЁпCD=5ЃЌЁрDC=DGЃЌЁпDHЁЭCGЃЌЁрGH=CH=3ЃЌдкRtЁїCDHжаЃЌDH=![]() =
=![]() =4ЃЌЁпSЁїDGC=
=4ЃЌЁпSЁїDGC=![]() CGDH=
CGDH=![]() DGCJЃЌЁрCJ=
DGCJЃЌЁрCJ=![]() ЃЌЁрsinЁЯCDJ=
ЃЌЁрsinЁЯCDJ=![]() ЃЌЁпЁЯCDJ=75ЁуЃЌЁргыsin75Ёу=
ЃЌЁпЁЯCDJ=75ЁуЃЌЁргыsin75Ёу=![]() УЌЖмЃЌЁрМйЩшВЛГЩСЂЃЌЁрЕуGВЛЪЧADЕФжаЕуЃЎ
УЌЖмЃЌЁрМйЩшВЛГЩСЂЃЌЁрЕуGВЛЪЧADЕФжаЕуЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћвЛИіЗжЪНЕФЗжзгЛђЗжФИПЩвдвђЪНЗжНтЃЌЧветИіЗжЪНВЛПЩдМЗжЃЌФЧУДЮвУЧГЦет
ИіЗжЪНЮЊЁАКЭаГЗжЪНЁБ.
ЃЈ1ЃЉЯТСаЗжЪН:Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм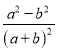 . ЦфжаЪЧЁАКЭаГЗжЪНЁБЪЧ (ЬюаДађКХМДПЩ)ЃЛ
. ЦфжаЪЧЁАКЭаГЗжЪНЁБЪЧ (ЬюаДађКХМДПЩ)ЃЛ
ЃЈ2ЃЉШє![]() ЮЊе§ећЪ§ЃЌЧв
ЮЊе§ећЪ§ЃЌЧв![]() ЮЊЁАКЭаГЗжЪНЁБЃЌЧыаДГі
ЮЊЁАКЭаГЗжЪНЁБЃЌЧыаДГі![]() ЕФжЕ;
ЕФжЕ;
ЃЈ3ЃЉдкЛЏМђ![]() ЪБЃЌ
ЪБЃЌ
аЁЖЋКЭаЁЧПЗжБ№НјааСЫШчЯТШ§ВНБфаЮ:
аЁЖЋЃК ![]()
![]()
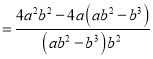
аЁЧПЃК ![]()
![]()
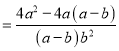
ЯдШЛЃЌаЁЧПРћгУСЫЦфжаЕФКЭаГЗжЪН, ЕкШ§ВНЫљЕУНсЙћБШаЁЖЋЕФНсЙћМђЕЅЃЌ
двђЪЧЃК ЃЌ
ЧыФуНгзХаЁЧПЕФЗНЗЈЭъГЩЛЏМђ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНёФъФИХЎСНШЫЕФФъСфКЭЮЊ60ЫъЃЌ10ФъЧАФИЧзЕФФъСфЪЧХЎЖљЕФ7БЖЃЌдђНёФъФИЧзЁЂХЎЖљЕФФъСфИїЪЧЖрЩйЫъЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуBЁЂEЗжБ№дкACЁЂDFЩЯЃЌAFЗжБ№НЛBDЁЂCEгкЕуMЁЂNЃЌЁЯA=ЁЯFЃЌЁЯ1=ЁЯ2ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮBCEDЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉвбжЊDE=2ЃЌСЌНгBNЃЌШєBNЦНЗжЁЯDBCЃЌЧѓCNЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЃЈ1ЃЌ1ЃЉЃЌBЃЈ3ЃЌ2ЃЉЃЌНЋЕуAЯђзѓЦНвЦСНИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ4ИіЕЅЮЛЕУЕНЕуCЃЎ
ЃЈ1ЃЉаДГіЕуCзјБъЃЛ
ЃЈ2ЃЉЧѓЁїABCЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
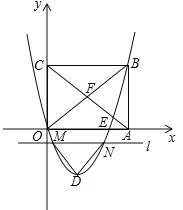
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФБпOAЁЂOCЗжБ№дкxжсЁЂyжсЩЯЃЌЕуBзјБъЮЊЃЈ4ЃЌtЃЉЃЈtЃО0ЃЉЃЌЖўДЮКЏЪ§![]() ЃЈbЃМ0ЃЉЕФЭМЯѓОЙ§ЕуBЃЌЖЅЕуЮЊЕуDЃЎ
ЃЈbЃМ0ЃЉЕФЭМЯѓОЙ§ЕуBЃЌЖЅЕуЮЊЕуDЃЎ
ЃЈ1ЃЉЕБt=12ЪБЃЌЖЅЕуDЕНxжсЕФОрРыЕШгк ЃЛ
ЃЈ2ЃЉЕуEЪЧЖўДЮКЏЪ§![]() ЃЈbЃМ0ЃЉЕФЭМЯѓгыxжсЕФвЛИіЙЋЙВЕуЃЈЕуEгыЕуOВЛжиКЯЃЉЃЌЧѓOEEAЕФзюДѓжЕМАШЁЕУзюДѓжЕЪБЕФЖўДЮКЏЪ§БэДяЪНЃЛ
ЃЈbЃМ0ЃЉЕФЭМЯѓгыxжсЕФвЛИіЙЋЙВЕуЃЈЕуEгыЕуOВЛжиКЯЃЉЃЌЧѓOEEAЕФзюДѓжЕМАШЁЕУзюДѓжЕЪБЕФЖўДЮКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉОиаЮOABCЕФЖдНЧЯпOBЁЂACНЛгкЕуFЃЌжБЯпlЦНаагкxжсЃЌНЛЖўДЮКЏЪ§![]() ЃЈbЃМ0ЃЉЕФЭМЯѓгкЕуMЁЂNЃЌСЌНгDMЁЂDNЃЌЕБЁїDMNЁеЁїFOCЪБЃЌЧѓtЕФжЕЃЎ
ЃЈbЃМ0ЃЉЕФЭМЯѓгкЕуMЁЂNЃЌСЌНгDMЁЂDNЃЌЕБЁїDMNЁеЁїFOCЪБЃЌЧѓtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШБпЁїA1C1C2ЕФжмГЄЮЊ1ЃЌзїC1D1ЁЭA1C2гкD1ЃЌдкC1C2ЕФбгГЄЯпЩЯШЁЕуC3ЃЌЪЙD1C3=D1C1ЃЌСЌНгD1C3ЃЌвдC2C3ЮЊБпзїЕШБпЁїA2C2C3ЃЛзїC2D2ЁЭA2C3гкD2ЃЌдкC2C3ЕФбгГЄЯпЩЯШЁЕуC4ЃЌЪЙD2C4=D2C2ЃЌСЌНгD2C4ЃЌвдC3C4ЮЊБпзїЕШБпЁїA3C3C4ЃЛЁЧвЕуA1ЃЌA2ЃЌA3ЃЌЁЖМдкжБЯпC1C2ЭЌВрЃЌШчДЫЯТШЅЃЌдђЁїA1C1C2ЃЌЁїA2C2C3ЃЌЁїA3C3C4ЃЌЁЃЌЁїAnCnCn+1ЕФжмГЄКЭЮЊ______ЃЎЃЈnЁн2ЃЌЧвnЮЊећЪ§ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЯпЖЮABКЭЩфЯпBMНЛгкЕуBЃЎ
ЃЈ1ЃЉРћгУГпЙцЭъГЩвдЯТзїЭМЃЌВЂБЃСєзїЭМКлМЃЃЈВЛаДзїЗЈЃЉ
ЂйдкЩфЯпBMЩЯзївЛЕуCЃЌЪЙAC=ABЃЛ
ЂкзїЁЯABM ЕФНЧЦНЗжЯпНЛACгкDЕуЃЛ
ЂлдкЩфЯпCMЩЯзївЛЕуEЃЌЪЙCE=CDЃЌСЌНгDE.
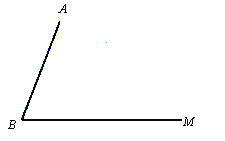
ЃЈ2ЃЉдкЃЈ1ЃЉЫљзїЕФЭМаЮжаЃЌВТЯыЯпЖЮBDгыDEЕФЪ§СПЙиЯЕЃЌВЂжЄУїжЎЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОнБЈЕМЃЌЮвЪЁХЉзїЮяНеИЫЕФзЪдДОоДѓЃЌЕЋКЯРэРћгУСПЪЎЗжгаЯоЃЌ2006ФъЕФРћгУТЪжЛга30%ЃЌДѓВПЗжНеИЫБЛжБНгЗйЩеСЫЃЌМйЖЈЮвЪЁУПФъВњГіЕФХЉзїЮяНеИЫзмСПВЛБфЃЌЧвКЯРэРћгУЕФдіГЄТЪЯрЭЌЃЌвЊЪЙ2008ФъЕФРћгУТЪЬсИпЕН60%ЃЌЧѓУПФъЕФдіГЄТЪЁЃЃЈШЁ![]() Ёж1.41ЃЉ
Ёж1.41ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com