
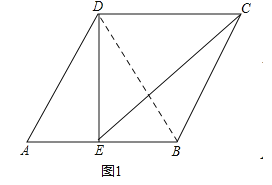
【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
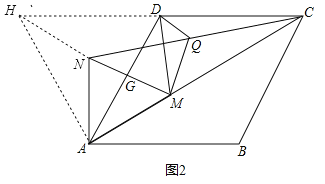
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

【答案】(1)2![]() (2)证明见解析
(2)证明见解析
【解析】试题分析:(1)如图1,连接对角线BD,先证明△ABD是等边三角形,根据E是AB的中点,由等腰三角形三线合一得:DE⊥AB,利用勾股定理依次求DE和EC的长;
(2)如图2,作辅助线,构建全等三角形,先证明△ADH是等边三角形,再由△AMN是等边三角形,得条件证明△ANH≌△AMD(SAS),则HN=DM,根据DQ是△CHN的中位线,得HN=2DQ,由等量代换可得结论.
试题解析:解:(1)如图1,连接BD,则BD平分∠ABC,∵四边形ABCD是菱形,∴AD∥BC,∴∠A+∠ABC=180°,∵∠A=60°,∴∠ABC=120°,∴∠ABD=![]() ∠ABC=60°,∴△ABD是等边三角形,∴BD=AD=4,∵E是AB的中点,∴DE⊥AB,由勾股定理得:DE=
∠ABC=60°,∴△ABD是等边三角形,∴BD=AD=4,∵E是AB的中点,∴DE⊥AB,由勾股定理得:DE=![]() =
=![]() ,∵DC∥AB,∴∠EDC=∠DEA=90°,在Rt△DEC中,DC=4,EC=
,∵DC∥AB,∴∠EDC=∠DEA=90°,在Rt△DEC中,DC=4,EC=![]() =
=![]() =
=![]() ;
;
(2)如图2,延长CD至H,使CD=DH,连接NH、AH,∵AD=CD,∴AD=DH,∵CD∥AB,∴∠HDA=∠BAD=60°,∴△ADH是等边三角形,∴AH=AD,∠HAD=60°,∵△AMN是等边三角形,∴AM=AN,∠NAM=60°,∴∠HAN+∠NAG=∠NAG+∠DAM,∴∠HAN=∠DAM,在△ANH和△AMD中,∵AH=AD,∠HAN=∠DAM,AN=AM,∴△ANH≌△AMD(SAS),∴HN=DM,∵D是CH的中点,Q是NC的中点,∴DQ是△CHN的中位线,∴HN=2DQ,∴DM=2DQ.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于点E,AE平分∠BAC,AO=CO,AD=DC=2,下面结论:①AC=2AB;②AB=![]() ;③S△ADC=2S△ABE;④BO⊥AE.其中正确的有( )
;③S△ADC=2S△ABE;④BO⊥AE.其中正确的有( )
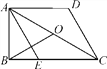
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.

(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.
(1)试探究BE与BF的数量关系,并证明你的结论;
(2)求EF的最大值与最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④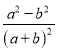 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()
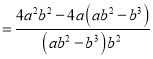
小强: ![]()
![]()
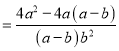
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式![]() +(b﹣3)2=0,(c﹣4)2≤0
+(b﹣3)2=0,(c﹣4)2≤0

(1)求a、b、c的值;
(2)如果在第二象限内有一点P(﹣m,![]() ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com