
【题目】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AE∥CD交BC于点E,AE平分∠BAC,AO=CO,AD=DC=2,下面结论:①AC=2AB;②AB=![]() ;③S△ADC=2S△ABE;④BO⊥AE.其中正确的有( )
;③S△ADC=2S△ABE;④BO⊥AE.其中正确的有( )
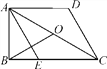
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】试题分析:∵AD∥BC,AE∥CD,
∴四边形AECD是平行四边形.
∵AD=DC,
∴四边形AECD是菱形,
∴AE=EC=CD=AD=2,
∴∠2=∠3.
∵∠1=∠2,
∴∠1=∠2=∠3.
∵∠ABC=90°,
∴∠1+∠2+∠3=90°,
∴∠1=∠2=∠3=30°,
∴BE=![]() AE=1,AC=2AB.①正确;
AE=1,AC=2AB.①正确;
在Rt△ABE中,由勾股定理,得
AB=![]() =
=![]() =
=![]() ,②正确;
,②正确;
∵O是AC的中点,∠ABC=90°,
∴BO=AO=CO=![]() AC.
AC.
∵∠1=∠2=∠3=30°,
∴∠BAO=60°,
∴△ABO为等边三角形.
∵∠1=∠2,
∴AE⊥BO.④正确;
∵S△ADC=S△AEC=![]() AB·CE ,S△ABE=
AB·CE ,S△ABE=![]() AB·BE,
AB·BE,
∵CE=2,BE=1,
∴CE=2BE,
∴S△ACE=![]() AB·2BE
AB·2BE
=2×![]() AB·BE ,
AB·BE ,
∴S△ACE=2S△ABE,
∴S△ADC=2S△ABE.③正确.
∴正确的个数有4个.
故选D.


科目:初中数学 来源: 题型:
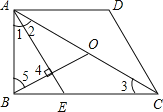
【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,H为BC上一点,且BH=BA交AC于点F,连接FH.
⑴求证:AE=FH;
⑵作EG//BC交AC于点G若AG=5,AC=8,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是( )

A. ②④ B. ①③ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,菱形OABC的OC边落在x轴上,∠AOC=60°,OA=60![]() .若菱形OABC内部(边界及顶点除外)的一格点P(x,y)满足:x2﹣y2=90x﹣90y,就称格点P为“好点”,则菱形OABC内部“好点”的个数为( )
.若菱形OABC内部(边界及顶点除外)的一格点P(x,y)满足:x2﹣y2=90x﹣90y,就称格点P为“好点”,则菱形OABC内部“好点”的个数为( )
(注:所谓“格点”,是指在平面直角坐标系中横、纵坐标均为整数的点.)
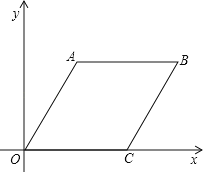
A. 145 B. 146 C. 147 D. 148
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适合于全面调查方式的是( )
A.调查春节联欢晚会的收视率B.调查某班学生的身高情况
C.调查一批节能灯的使用寿命D.调查某批次汽车的抗撞能力
查看答案和解析>>
科目:初中数学 来源: 题型:
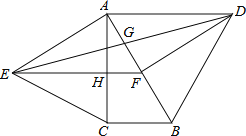
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com