Question

【题目】在平面直角坐标系中，菱形OABC的OC边落在x轴上，∠AOC=60°，OA=60．若菱形OABC内部（边界及顶点除外）的一格点P（x，y）满足：x2﹣y2=90x﹣90y，就称格点P为“好点”，则菱形OABC内部“好点”的个数为（　　）

（注：所谓“格点”，是指在平面直角坐标系中横、纵坐标均为整数的点．）

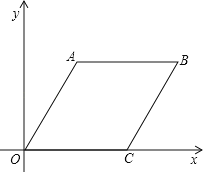
A. 145 B. 146 C. 147 D. 148

Answer 1

【答案】A

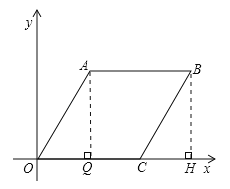
【解析】解：过A作AQ⊥OC于Q，过B作BH⊥X轴于H，∵∠A0C=60°，OA=，∴∠OAQ=30°，∴OQ=，由勾股定理得：AQ=90，∵x2﹣y2=90x﹣90y，∴（x﹣y）（x+y﹣90）=0，∴x=y，x+y=90，BH=90 OA：y′=x

（1）y=x时，令y=90 则x=90，作直线y=x的图象，交AB于D，∵AQ=90，∴D（90，90）．

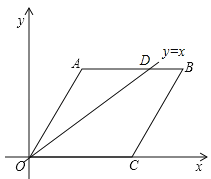
∵边界及顶点除外

∴y=x时有90﹣1=89个点符合（D点除外），（2）y=﹣x+90时，∵直线OA的解析式为y′=x，∴令y=y′则x=45（﹣1）．

∵≈1.732，∴x≈32.9（取x=33），则直线OA于直线y=﹣x+90的交点是（45﹣45，135﹣45），再令y=0 则x=90，∵边界及顶点除外，∴y=﹣x+90时有90﹣32﹣1=57个点符合，∴有57+89﹣1=145个点符合，故选A．