练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在五边形ABCDE中，AB=AC=AD=AE， 且AB∥ED，∠AED=70°，则∠DCB=（　　）

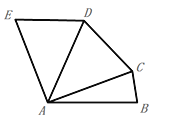
    A. 70° B. 165° C. 155° D. 145°

    【答案】D

    【解析】∵AB∥ED，

    ∴∠EAB＋∠AED=180°，

    ∵∠AED=70°，

    ∴∠EAB=110°，

    ∵AD=AE，∠AED=70°，

    ∴∠DAE=40°，

    ∴∠BAD=∠EAB -∠DAE=70°，

    在四边形ABCD中，∠BAD+∠ABC+∠BCD+∠ADC=360°，

    ∴∠ABC+∠BCD+∠ADC=290°，

    ∵AB=AC=AD，

    ∴∠B=∠ACB，∠ACD=∠ADC，

    ∵∠B+∠ACB+∠ACD+∠ADC=290°，

    ∴∠ACB+∠ACD=145°，即∠DCB=145°．

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若A＝（x+y）2，B＝（x﹣y）2，则A﹣B＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】钟表上的时间是2时35分，此时时针与分针所成的夹角是_____度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年母女两人的年龄和为60岁，10年前母亲的年龄是女儿的7倍，则今年母亲、女儿的年龄各是多少岁？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图甲，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作等腰直角三角形ADE，AD=AE，∠DAE=90.解答下列问题：

    (1) 如果AB=AC，∠BAC=90．

    ①当点D在线段BC上时（与点B不重合），如图乙，线段CE、BD之间的位置关系为，数量关系为．（不用证明）

    ②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？

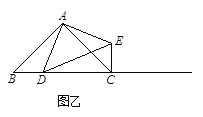
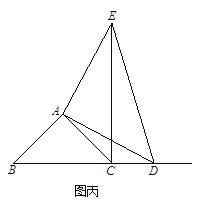
    (2) 如果AB≠AC，∠BAC≠90，点D在线段BC上运动．

    试探究：当△ABC满足一个什么条件时，CE⊥BD（点C、E重合除外）？画出相应的图形，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A=∠F，∠1=∠2．

    （1）求证：四边形BCED是平行四边形；

    （2）已知DE=2，连接BN，若BN平分∠DBC，求CN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，点A（1，1），B（3，2），将点A向左平移两个单位，再向上平移4个单位得到点C．

    （1）写出点C坐标；

    （2）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△A1C1C2的周长为1，作C1D1⊥A1C2于D1，在C1C2的延长线上取点C3，使D1C3=D1C1，连接D1C3，以C2C3为边作等边△A2C2C3；作C2D2⊥A2C3于D2，在C2C3的延长线上取点C4，使D2C4=D2C2，连接D2C4，以C3C4为边作等边△A3C3C4；…且点A1，A2，A3，…都在直线C1C2同侧，如此下去，则△A1C1C2，△A2C2C3，△A3C3C4，…，△AnCnCn+1的周长和为______．（n≥2，且n为整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】3的相反数是（ ）

    A.0B.3C.-3D.6

    查看答案和解析>>

    同步练习册答案