
،¾جâؤ؟،؟بçح¼¼×£¬شع،÷ABCضذ£¬،دACBخھبٌ½ا£®µمDخھةندكBCةدز»¶¯µم£¬ء¬½سAD£¬زشADخھز»±كازشعADµؤسز²à×÷µبرüض±½اب½اذخADE£¬AD=AE£¬،دDAE=90.½â´ًدآءذختجâ£؛
(1) بç¹ûAB=AC£¬،دBAC=90£®
¢ظµ±µمDشعدك¶خBCةدت±£¨سëµمB²»ضط؛د£©£¬بçح¼زز£¬دك¶خCE،¢BDض®¼نµؤخ»ضأ¹طدµخھ£¬تء؟¹طدµخھ£®£¨²»سأض¤أ÷£©
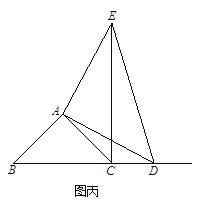
¢عµ±µمDشعدك¶خBCµؤرس³¤دكةدت±£¬بçح¼±û£¬¢ظضذµؤ½لآغتا·ٌبشب»³ةء¢£¬خھت²أ´£؟

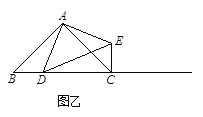
(2) بç¹ûAB،ظAC£¬،دBAC،ظ90£¬µمDشعدك¶خBCةدشث¶¯£®
تشج½¾؟£؛µ±،÷ABCآْ×مز»¸ِت²أ´جُ¼ت±£¬CE،حBD£¨µمC،¢Eضط؛د³ح⣩£؟»³ِدàس¦µؤح¼ذخ£¬²¢ثµأ÷ہيسة£®
،¾´ً°¸،؟¼û½âخِ
،¾½âخِ،؟تشجâ·ضخِ£؛£¨1£©¢ظ¸ù¾ف،دBAD=،دCAE£¬BA=CA£¬AD=AE£¬شثسأ،°SAS،±ض¤أ÷،÷ABD،ص،÷ACE£¬¸ù¾فب«µبب½اذخذشضتµأ³ِ¶شس¦±كدàµب£¬¶شس¦½ادàµب£¬¼´؟ةµأµ½دك¶خCE،¢BDض®¼نµؤ¹طدµ£»¢عدب¸ù¾ف،°SAS،±ض¤أ÷،÷ABD،ص،÷ACE£¬شظ¸ù¾فب«µبب½اذخذشضتµأ³ِ¶شس¦±كدàµب£¬¶شس¦½ادàµب£¬¼´؟ةµأµ½¢ظضذµؤ½لآغبشب»³ةء¢£»
£¨2£©دب¹µمA×÷AG،حAC½»BCسعµمG£¬»³ِ·û؛دزھاَµؤح¼ذخ£¬شظ½ل؛دح¼ذخإذ¶¨،÷GAD،ص،÷CAE£¬µأ³ِ¶شس¦½ادàµب£¬¼´؟ةµأ³ِ½لآغ£®
تشجâ½âخِ£؛£¨1£©¢ظCEسëBDخ»ضأ¹طدµتاCE،حBD£¬تء؟¹طدµتاCE=BD.
ہيسة£؛بçح¼زز,

،ك،دBAD=90،م،دDAC,،دCAE=90،م،دDAC£¬
،à،دBAD=،دCAE.
سضBA=CA£¬AD=AE£¬
،à،÷ABD،ص،÷ACE(SAS)
،à،دACE=،دB=45،مازCE=BD.
،ك،دACB=،دB=45،م£¬
،à،دECB=45،م+45،م=90،م£¬¼´CE،حBD.
¹ت´ً°¸خھ£؛CE،حBD£»CE=BD.
¢عµ±µمDشعBCµؤرس³¤دكةدت±,¢ظµؤ½لآغبش³ةء¢.
بçح¼±û,

،ك،دDAE=90،م,،دBAC=90،م£¬
،à،دDAE=،دBAC£¬
،à،دDAB=،دEAC£¬
سضAB=AC£¬AD=AE£¬
،à،÷DAB،ص،÷EAC£¬
،àCE=BD£¬از،دACE=،دABD.
،ك،دBAC=90،م£¬AB=AC£¬
،à،دABC=45،م£¬
،à،دACE=45،م£¬
،à،دBCE=،دACB+،دACE=90،م£¬
¼´CE،حBD£»
£¨2£©بçح¼¶،ثùت¾,µ±،دBCA=45،مت±,CE،حBD.
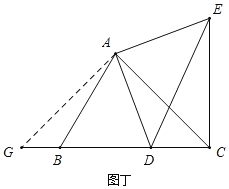
ہيسة£؛¹µمA×÷AG،حAC½»BCسعµمG£¬
،àAC=AG,،دAGC=45،م£¬
¼´،÷ACGتاµبرüض±½اب½اذخ£¬
،ك،دGAD+،دDAC=90،م=،دCAE+،دDAC£¬
،à،دGAD=،دCAE£¬
سض،كDA=EA£¬
،à،÷GAD،ص،÷CAE£¬
،à،دACE=،دAGD=45،م£¬
،à،دBCE=،دACB+،دACE=90،م£¬
¼´CE،حBD.



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟دآءذ¼ئثمصب·µؤتا£¨،،،،£©
A.2a©پa£½2B.5x©پ3x£½2x
C.y2©پy£½yD.3a2+2a2£½5a4
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟¹غ²ىدآءذµبت½£؛
µعز»¸ِµبت½£؛ ![]()
µع¶¸ِµبت½£؛ ![]()
µعب¸ِµبت½£؛ ![]()
µعثؤ¸ِµبت½£؛ ![]()
شٍت½×س![]() __________________£»
__________________£»
سأ؛¬nµؤ´ْتت½±يت¾µعn¸ِµبت½£؛ ![]() ____________________________£»
____________________________£»
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ£؛بçح¼£¬Rt،÷ABCضذ£¬،دBAC=90،م
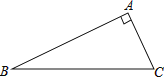
£¨1£©°´زھاَ×÷ح¼£؛£¨±£ءô×÷ح¼؛غ¼££©
¢ظرس³¤BCµ½µمD£¬ت¹CD=BC£»
¢عرس³¤CAµ½µمE£¬ت¹AE=2CA£»
¢غء¬½سAD£¬BE²¢²آدëدك¶خ ADسëBEµؤ´َذ،¹طدµ£»
£¨2£©ض¤أ÷£¨1£©ضذؤم¶شدك¶خADسëBE´َذ،¹طدµµؤ²آد룮
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شعخه±كذخABCDEضذ£¬AB=AC=AD=AE£¬ ازAB،خED£¬،دAED=70،م£¬شٍ،دDCB=£¨،،،،£©
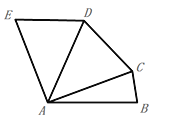
A. 70،م B. 165،م C. 155،م D. 145،م
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟¼ئثم£؛a2(b1) 2½ل¹ûصب·µؤتا£¨ £©
A.a2b22b+1B.a2b22b1
C.a2b2+2b1D.a2b2+2b+1
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬،÷ABCضذ£¬،دACB£½90،م£¬AC£½BC£¬AEتاBC±كةدµؤضذدك£¬¹µمC×÷CF،حAE£¬´¹×مخھF£¬¹B×÷BD،حBC½»CFµؤرس³¤دكسعD£»بôAC£½12cm£¬اَBDµؤ³¤£»
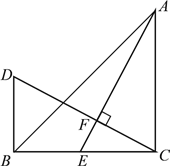
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com