
【题目】已知:如图,Rt△ABC中,∠BAC=90°
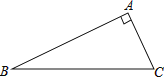
(1)按要求作图:(保留作图痕迹)
①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段 AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
【答案】见解析
【解析】试题分析:(1)根据基本作图,作一条线段等于已知线段的作图方法就可以作出图形;
(2)延长AC到点F,使CF=AF,连接BF,证明△ACD≌△FCB,就有AD=FB,进而得出AE=AF,就可以得出BE=BF,从而结论AD=BE.
试题解析:(1)由题意,得作图如下: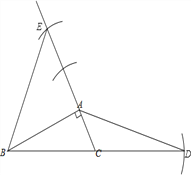
(2)延长AC到点F,使CF=AF,连接BF,
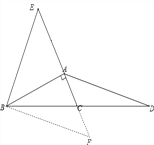
在△ACD和△FCB中,
CD=CB,∠ACD=∠FCB,AC=FC,
∴△ACD≌△FCB(SAS)
∴AD=FB.
∵CF=AF,
∴AF=2AC.
∵AE=2CA,
∴AF=AE,
∵∠BAC=90°,
∴AB⊥EF,
∴AB是EF的垂直平分线,
∴BE=BF,
∴AD=BE.


科目:初中数学 来源: 题型:
【题目】探究归纳题:
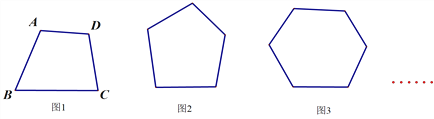
(1)试验分析:
如图1,经过A点可以做__________条对角线;同样,经过B点可以做__________条;经过C点可以做__________条;经过D点可以做__________条对角线.
通过以上分析和总结,图1共有___________条对角线.
(2)拓展延伸:
运用(1)的分析方法,可得:
图2共有_____________条对角线;
图3共有_____________条对角线;
(3)探索归纳:
对于n边形(n>3),共有_____________条对角线.(用含n的式子表示)
(4)特例验证:
十边形有__________________对角线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张对边互相平行的纸条折成如图,EF是折痕,若∠EFB=34°则下列结论正确的有( )
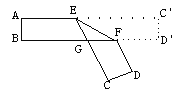
①∠CEF=34°②∠AEC=112°;③∠BGE=68°;④∠BFD=116°.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点E、F分别在平行四边形ABCD的边BC、AD上,BE=DF,点P在边AB上,AP:PB=1:n(n>1),过点P且平行于AD的直线l将△ABE分成面积为S1、S2的两部分,将△CDF分成面积为S3、S4的两部分(如图),下列四个等式:
①![]()
②![]()
③![]()
④![]()
其中成立的有( )
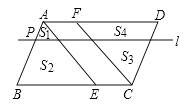
A. ①②④ B. ②③ C. ②③④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
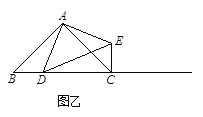
【题目】如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90.解答下列问题:
(1) 如果AB=AC,∠BAC=90.
①当点D在线段BC上时(与点B不重合),如图乙,线段CE、BD之间的位置关系为,数量关系为.(不用证明)
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?

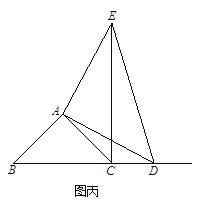
(2) 如果AB≠AC,∠BAC≠90,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外)?画出相应的图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.
(1)小丽参加实验A考查的概率是 ;
(2)用列表或画树状图的方法求小明、小丽都参加实验A考查的概率;
(3)他们三人都参加实验A考查的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
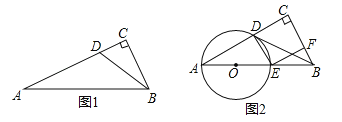
【题目】如图1,Rt△ACB 中,∠C=90°,点D在AC上,∠CBD=∠A,过A、D两点的圆的圆心O在AB上.
(1)利用直尺和圆规在图1中画出⊙O(不写作法,保留作图痕迹,并用黑色水笔把线条描清楚);
(2)判断BD所在直线与(1)中所作的⊙O的位置关系,并证明你的结论;
(3)设⊙O交AB于点E,连接DE,过点E作EF⊥BC,F为垂足,若点D是线段AC的黄金分割点(即![]() ),如图2,试说明四边形DEFC是正方形.
),如图2,试说明四边形DEFC是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
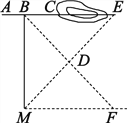
【题目】如图,沿AC方向开山修路,为了加快施工进度,要在山的另一边同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD,并延长使DF=BD,过F点作AB的平行线段MF,连接MD,并延长,在其延长线上取一点E,使DE=DM,在E点开工就能使A、C、E成一条直线,请说明其中的道理;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com