
����Ŀ����ͼ1��Rt��ACB �У���C=90������D��AC�ϣ���CBD=��A����A��D�����Բ��Բ��O��AB�ϣ�
��1������ֱ�ߺ�Բ����ͼ1�л�����O����д������������ͼ�ۼ������ú�ɫˮ�ʰ��������������
��2���ж�BD����ֱ���루1������������O��λ�ù�ϵ����֤����Ľ��ۣ�
��3������O��AB�ڵ�E������DE������E��EF��BC��FΪ���㣬����D���߶�AC�Ļƽ�ָ�㣨��![]() ������ͼ2����˵���ı���DEFC�������Σ�
������ͼ2����˵���ı���DEFC�������Σ�
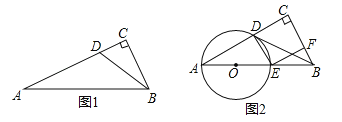
���𰸡���1����ͼ����������2��BD���O���У���3��֤����������
�������������������1����ͼ1�����߶�AD�Ĵ�ֱƽ���߽�AB��O��Ȼ���Ե�OΪԲ�ģ�OAΪ�뾶��Բ��
��2������OD����ͼ1��������A=��ODA����CBD=��A�õ���CBD=��ODA�����֤����ODB=90����Ȼ��������ߵ��ж��������ж�BDΪ��O�����ߣ�
��3����֤����CDB�ס�CBA�õ�CB2=CDCA���ٸ��ݻƽ�ָ�Ķ���õ�AD2=CDAC����AD=CB������֤����ADE�ա�BCD�õ�DE=DC�����ı���CDEFΪ���Σ�Ȼ����������ε��ж��������ж��ı���DEFC�������Σ�
����������⣺��1����ͼ1����OΪ������

��2��BD����O���У��������£�
����OD����ͼ1����OA=OD�����A=��ODA���ߡ�CBD=��A�����CBD=��ODA���ߡ�C=90�������CBD+��CDB=90�������ODA+��CDB=90�������ODB=90������OD��BD����BDΪ��O�����ߣ�
��3���ߡ�CBD=��A����DCB=��BCA�����CDB�ס�CBA����CD��CB=CB��CA����CB2=CDCA������D���߶�AC�Ļƽ�ָ�㣬��AD2=CDAC����AD=CB����AEΪֱ�������ADE=90��������ADE����BCD�����ߡ�A=��CBD��AD=BC����ADE=��C�����ADE�ա�BCD����DE=DC����EF��BC�����EFC=90�������ı���CDEFΪ���Σ����ı���DEFC�������Σ�




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���У�������
����������������ɵ�ͼ�ν����ǣ�
������֮�䣬�߶���̣�
���������Ƚϴ�С������ֵ��ķ���С��
������ʽ�Ͷ���ʽ������ʽ��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��Rt��ABC�У���BAC=90��
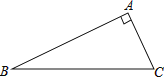
��1����Ҫ����ͼ����������ͼ�ۼ���
���ӳ�BC����D��ʹCD=BC��
���ӳ�CA����E��ʹAE=2CA��
������AD��BE�������߶� AD��BE�Ĵ�С��ϵ��
��2��֤����1��������߶�AD��BE��С��ϵ�IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���B=90����AB=3cm��BC=4cm����D��AC�ϣ�AD=1cm����P�ӵ�A��������AB�����˶�����Q�ӵ�C��������C��B��A��C��·�������˶�������ͬʱ��������B�㴦�״�������P���˶��ٶ�ÿ�������2cm������B��C��A��·�������˶�����Q�����ٶȲ��䣬��������ԭ·�������˶���������D�㴦�ٴ�������ֹͣ�˶������Pԭ�����ٶ�Ϊxcm/s��
��1����Q���ٶ�Ϊ cm/s���ú�x�Ĵ���ʽ��ʾ����
��2�����Pԭ�����ٶȣ�
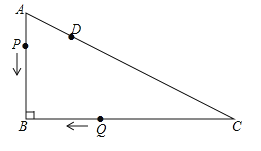
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺a2(b1) 2�����ȷ���ǣ� ��
A.a2b22b+1B.a2b22b1
C.a2b2+2b1D.a2b2+2b+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
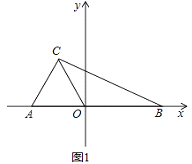
����Ŀ����ƽ��ֱ������ϵ�У�A��a��0����B��b��0����C����1��2������ͼ1������ ![]()
��1����a��b��ֵ��
��2������x����������ϴ���һ��M��ʹ������COM�������������ABC�������һ�룬�����M�����ꣻ
���������������λ���Ƿ���ڵ�M��ʹ������COM�����������ABC�������һ����Ȼ����? �����ڣ���ֱ��д�����������ĵ�M�����ꣻ
��3����ͼ2������C��CD��y�ύy���ڵ�D����PΪ�߶�CD�ӳ����ϵ�һ���㣬����OP��OEƽ�֡�AOP��OF��OE������P�˶�ʱ�� ![]() ��ֵ�Ƿ��ı䣿�����䣬����ֵ�����ı䣬˵�����ɣ�
��ֵ�Ƿ��ı䣿�����䣬����ֵ�����ı䣬˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A.һ���������������Ǹ���
B.���ĸ�������-1
C.�κ����ľ���ֵ��������
D.0������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��СӢͬʱ���ס�����ö�ʵؾ��ȵ����������ӣ��Ǽ����ӳ���һ�������Ϊx�������ӳ���һ�������Ϊy��������ȷ����P��һ������(x��y)����ô��P����˫����y��![]() �ϵĸ���Ϊ________.
�ϵĸ���Ϊ________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com