
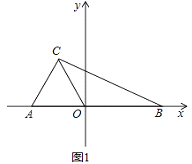
����Ŀ����ƽ��ֱ������ϵ�У�A��a��0����B��b��0����C����1��2������ͼ1������ ![]()
��1����a��b��ֵ��
��2������x����������ϴ���һ��M��ʹ������COM�������������ABC�������һ�룬�����M�����ꣻ
���������������λ���Ƿ���ڵ�M��ʹ������COM�����������ABC�������һ����Ȼ����? �����ڣ���ֱ��д�����������ĵ�M�����ꣻ
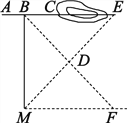
��3����ͼ2������C��CD��y�ύy���ڵ�D����PΪ�߶�CD�ӳ����ϵ�һ���㣬����OP��OEƽ�֡�AOP��OF��OE������P�˶�ʱ�� ![]() ��ֵ�Ƿ��ı䣿�����䣬����ֵ�����ı䣬˵�����ɣ�
��ֵ�Ƿ��ı䣿�����䣬����ֵ�����ı䣬˵�����ɣ�

���𰸡���1��a=-2��b=3����2�����������ĵ�M����Ϊ��2.5��0����-2.5��0����0��5����0��-5������3��![]() =2�����ɼ�������
=2�����ɼ�������
�����������������
��1����![]() �г�����a��b�ķ����飬���ɽ��a��b��ֵ��
�г�����a��b�ķ����飬���ɽ��a��b��ֵ��
��2�������������M������Ϊ��x��0������OM=![]() �������COM������ǡ�ABC�����һ�룬�г����̣��ⷽ�̽�ϵ�M��x��������ἴ����ô�ʱ��M�����ꣻ
�������COM������ǡ�ABC�����һ�룬�г����̣��ⷽ�̽�ϵ�M��x��������ἴ����ô�ʱ��M�����ꣻ
�������еĽ���ɵõ�M��x�Ḻ����ʱ�����ꣻ��M��y����ʱ�������M������Ϊ��0��y������ϡ�COM������ǡ�ABC�����һ�룬�г����̣��ⷽ�̼�����õ�M��y���ϵķ������������ꣻ
��3����������֤��OPD=��POB=2��BOF����DOE+��DOF=90������BOF+��DOF=90�����ɴ˿ɵõ���OPD=2��BOF=2��DOE���Ӷ��ɵ�![]() =2.
=2.
���������
��1����![]() ��
��
��![]() �����
�����![]() ��
��
��2��������1���н��ۿ�֪��A��B������ֱ�Ϊ��-2��0���ͣ�3��0����
��AB=5��
�֡ߵ�C������Ϊ��-1��2����
��S��ABC=![]() ��
��
����M��x����ʱ�����M������Ϊ��x��0������OM=![]() ��������ɵã�
��������ɵã�
![]() �����
�����![]() ��
��
����M��x��������ᣬ
����M��������2.5��0����
�������н��ۿ�֪����M��x��ĸ�����ʱ����M������Ϊ��-2.5��0����
����M��y����ʱ������ͼ�������M������Ϊ��0��y������OM=![]() ��������ɵã�
��������ɵã�
![]() ����ã�
����ã� ![]() ��
��
����ʱ��M������Ϊ��0��5����0��-5����
��������������M����������ʱ��������ֱ�Ϊ��2.5��0������-2.5��0������0��5���ͣ�0��-5����
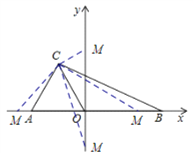
��3����ͼ2����CD��y�ᣬ
��CD��OB��
���OPD=��POB��
��OFƽ����POB��
���OPD=��POB=2��BOF��
��OE��OF��
���EOF=��DOB=90����
���DOE+��DOF=��DOF+��BOF=90����
���DOE=��BOF��
���POD=2��DOE��
��![]() =2.
=2.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�������⣺
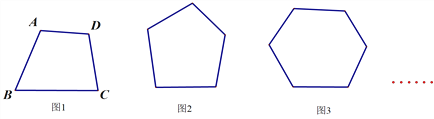
(1)���������
��ͼ1������A�������__________���Խ��ߣ�ͬ��������B�������__________��������C�������__________��������D�������__________���Խ���.
ͨ�����Ϸ������ܽᣬͼ1����___________���Խ���.
��2����չ���죺
���ã�1���ķ����������ɵã�
ͼ2����_____________���Խ��ߣ�
ͼ3����_____________���Խ��ߣ�
(3)̽�����ɣ�
����n����(n>3)������_____________���Խ��ߣ�(�ú�n��ʽ�ӱ�ʾ)
(4)������֤��
ʮ������__________________�Խ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ5�·ݾ����˰��꼶����ʵ�鿼�飬��A��B��������ʵ�飬�涨ÿλѧ��ֻ�μ�����һ��ʵ��Ŀ��飬����ѧ���Լ���ǩ��������Ŀ���ʵ�飬С����С����С�����μ��˱��ο��飮
��1��С���μ�ʵ��A����ĸ����� ��
��2�����б�����״ͼ�ķ�����С����С�����μ�ʵ��A����ĸ��ʣ�
��3���������˶��μ�ʵ��A����ĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
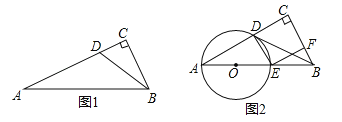
����Ŀ����ͼ1��Rt��ACB �У���C=90������D��AC�ϣ���CBD=��A����A��D�����Բ��Բ��O��AB�ϣ�
��1������ֱ�ߺ�Բ����ͼ1�л�����O����д������������ͼ�ۼ������ú�ɫˮ�ʰ��������������
��2���ж�BD����ֱ���루1������������O��λ�ù�ϵ����֤����Ľ��ۣ�
��3������O��AB�ڵ�E������DE������E��EF��BC��FΪ���㣬����D���߶�AC�Ļƽ�ָ�㣨��![]() ������ͼ2����˵���ı���DEFC�������Σ�
������ͼ2����˵���ı���DEFC�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ�������������⣬�ٰ�Ҫ�����������⣺
���⣺�����ʽy2+4y+8����Сֵ��
�⣺y2+4y+8=y2+4y+4+4=��y+2��2+4
����y+2��2��0
����y+2��2+4��4
��y2+4y+8����Сֵ��4��
��1�������ʽm2+m+4����Сֵ��
��2�������ʽ4��x2+2x�����ֵ��
��3��ij����С��Ҫ��һ��һ�߿�ǽ��ǽ��15m���Ŀյ��Ͻ�һ�������λ�ABCD����һ�߿�ǽ�����������ܳ�Ϊ20m��դ��Χ�ɣ���ͼ����AB=x��m�������ʣ���xȡ��ֵʱ�������������������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C=90����ADƽ����CAB��DE��AB��E����AC=6��BC=8��CD=3��

��1����DE�ij���
��2������ADB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������һ�������������1�������2��������170Ԫ����2�������1��������190Ԫ��
��1����һ�������һ��������ۼ۸��Ƕ���Ԫ��
��2��ѧУ���������������100������������������������������2�����������������ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AC����ɽ��·��Ϊ�˼ӿ�ʩ�����ȣ�Ҫ��ɽ����һ��ͬʱʩ��������ʦ����AC��ȡһ��B����Сɽ��ȡһ��D������BD�����ӳ�ʹDF��BD����F����AB��ƽ���߶�MF������MD�����ӳ��������ӳ�����ȡһ��E��ʹDE��DM����E�㿪������ʹA��C��E��һ��ֱ�ߣ���˵�����еĵ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������뽫һ��ϸľ���̶���ǽ�ϣ�������Ҫ��2�����ӣ���һ��ʵ˵���ˣ�_______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com