
【题目】观察下列等式:
第一个等式: ![]()
第二个等式: ![]()
第三个等式: ![]()
第四个等式: ![]()
则式子![]() __________________;
__________________;
用含n的代数式表示第n个等式: ![]() ____________________________;
____________________________;
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AD=2AB,点F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论中一定成立的是____.(把所有正确结论的序号都填在横线上)
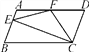
①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
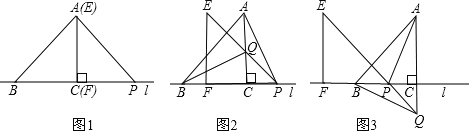
【题目】如图,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线 l上,边EF与边AC重合,且EF=FP.
(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连结AP,
BQ.猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;
(3)AP,BQ .你认为(2)中所猜想的BQ 与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张对边互相平行的纸条折成如图,EF是折痕,若∠EFB=34°则下列结论正确的有( )
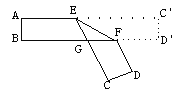
①∠CEF=34°②∠AEC=112°;③∠BGE=68°;④∠BFD=116°.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
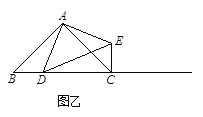
【题目】如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90.解答下列问题:
(1) 如果AB=AC,∠BAC=90.
①当点D在线段BC上时(与点B不重合),如图乙,线段CE、BD之间的位置关系为,数量关系为.(不用证明)
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?

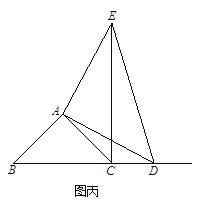
(2) 如果AB≠AC,∠BAC≠90,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外)?画出相应的图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(1,1),B(3,2),将点A向左平移两个单位,再向上平移4个单位得到点C.
(1)写出点C坐标;
(2)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com