
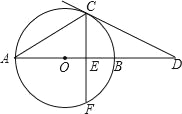
【题目】如图,AB为⊙O的直径,弦CF⊥AB于点E,CF=4![]() ,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
,过点C作⊙O的切线交AB的延长线于点D,∠D=30°,则OA的长为( )
A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 4
D. 4![]()
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】课间,小明拿着老师的等腰直角三角尺玩,不小心掉到两堆砖块之间,如图所示.
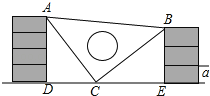
(1)求证:△ADC≌△CEB;
(2)已知DE=35cm,请你帮小明求出砖块的厚度a的大小(每块砖的厚度相同).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,P是直线AC上一点,AD⊥BP于D,以AD为边作等边△ADE(D,E在直线AC异侧).
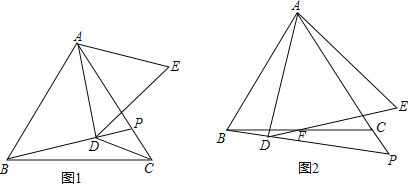
(1)如图1,若点P在边AC上,连CD,且∠BDC=150°,则![]() = ;(直接写结果)
= ;(直接写结果)
(2)如图2,若点P在AC延长线上,DE交BC于F求证:BF=CF;
(3)在图2中,若∠PBC=15°,AB=![]() ,请直接写出CP的长 .
,请直接写出CP的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
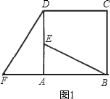
【题目】如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 延长线上的一点,
延长线上的一点,![]() .
.
![]() 求证
求证![]() ;
;
![]() 阅读下列材料:
阅读下列材料:
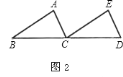
如图![]() ,把
,把![]() 沿直线
沿直线![]() 平行移动线段
平行移动线段![]() 的长度,可以变到
的长度,可以变到![]() 的位置;
的位置;
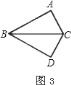
如图![]() ,以
,以![]() 为轴把
为轴把![]() 翻折
翻折![]() ,可以变到
,可以变到![]() 的位置;
的位置;
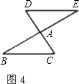
如图![]() ,以点
,以点![]() 为中心把
为中心把![]() 旋转
旋转![]() ,可以变到
,可以变到![]() 的位置.
的位置.
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在图![]() 中,可以通过平行移动、翻折、旋转中的哪一种方法使
中,可以通过平行移动、翻折、旋转中的哪一种方法使![]() 变到
变到![]() 的位置,
的位置,
答:________.
②指出图![]() 中,线段
中,线段![]() 与
与![]() 之间的关系.
之间的关系.
答:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,,
,,![]()
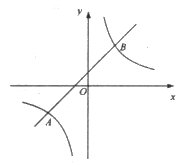
(1)求反比例函数与一次函数的函数表达式
(2)请结合图像直接写出不等式![]() 的解集;
的解集;
(3)若点P为x轴上一点,△ABP的面积为10,求点P的坐标,
查看答案和解析>>
科目:初中数学 来源: 题型:
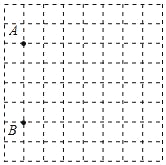
【题目】十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损.
(1)请在图中画出平面直角坐标系,并标出景点C的位置;
(2)平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.
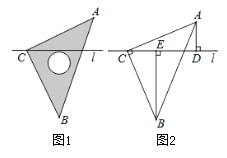
(1)△ACD与△CBE全等吗?说明你的理由.
(2)若AD=2,DE=3.5,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
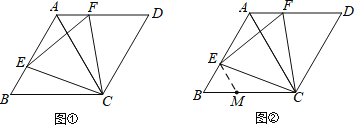
【题目】如图,在菱形ABCD中,∠B= 60°.
(1)如图①.若点E、F分别在边AB、AD上,且BE=AF,求证:△CEF是等边三角形.
(2)小明发现,当点E、F分别在边AB、AD上,且∠CEF=60°时,△CEF也是等边三角形,
并通过画图验证了猜想;小丽通过探索,认为应该以CE= EF为突破口,构造两个全等三角形:小倩受到小丽的启发,尝试在BC上截取BM =BE,并连接ME,如图②,很快就证明了△CEF是等边三角形.请你根据小倩的方法,写出完整的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
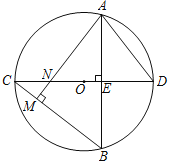
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com