
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌЁЯB= 60Ёу.
ЃЈ1ЃЉШчЭМЂй.ШєЕуEЁЂFЗжБ№дкБпABЁЂADЩЯЃЌЧвBE=AFЃЌЧѓжЄ:ЁїCEFЪЧЕШБпШ§НЧаЮ.
ЃЈ2ЃЉаЁУїЗЂЯжЃЌЕБЕуEЁЂFЗжБ№дкБпABЁЂADЩЯЃЌЧвЁЯCEF=60ЁуЪБЃЌЁїCEFвВЪЧЕШБпШ§НЧаЮЃЌ
ВЂЭЈЙ§ЛЭМбщжЄСЫВТЯы;аЁРіЭЈЙ§ЬНЫїЃЌШЯЮЊгІИУвдCE= EFЮЊЭЛЦЦПкЃЌЙЙдьСНИіШЋЕШШ§НЧаЮ:аЁйЛЪмЕНаЁРіЕФЦєЗЂЃЌГЂЪддкBCЩЯНиШЁBM =BEЃЌВЂСЌНгMEЃЌШчЭМЂкЃЌКмПьОЭжЄУїСЫЁїCEFЪЧЕШБпШ§НЧаЮ.ЧыФуИљОнаЁйЛЕФЗНЗЈЃЌаДГіЭъећЕФжЄУїЙ§ГЬ.
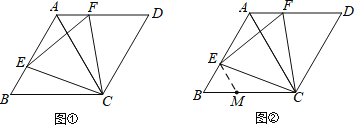
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉвзжЄЁїBECЁеЁїAFCЃЌМДПЩЕУжЄЃЛЃЈ2ЃЉЯШжЄЕУЁїBEMЪЧЕШБпШ§НЧаЮЃЌдйжЄЁїMECЁеAFEЃЌМДПЩEC=EFЃЌдйгЩЁЯCEF=60ЁуМДПЩжЄУї.
ЃЈ1ЃЉвђЮЊЫФБпаЮABCDЪЧСтаЮЃЌЫљвдAB= BC=CD=AD.
вђЮЊЁЯB=60ЁуЃЌЫљвдЁїABCЃЌЁїADCЖМЪЧЕШБпШ§НЧаЮ.
ЫљвдBC=ACЃЌЁЯB=ЁЯCAF=ЁЯACB=60ЁуЃЌ
гжвђЮЊBE=AFЃЌЫљвд.ЁїBECЁеЁїAFC(SAS)ЃЌЫљвдCE=CFЃЌЁЯECF=ЁЯBCA=60Ёу
ЫљвдЁїECFЪЧЕШБпШ§НЧаЮЃЌ
(2) вђЮЊBE=BMЃЌЁЯB= 60Ёу
ЫљвдЁїBEMЪЧЕШБпШ§НЧаЮ.
ЫљвдЁЯEMB=ЁЯBEM=60ЁуЃЌЁЯEMC=ЁЯAEM=120Ёу
вђЮЊAB= BCЃЌЁЯEAF120ЁуЃЌЫљвд.AE=CMЃЌЁЯEAF=ЁЯEM.
вђЮЊЁЯFEC=60ЁуЃЌЫљвдЁЯAEF+ЁЯCEM=60Ёу.
гжвђЮЊЁЯCEM+ЁЯECM=60ЁуЫљвдЁЯAEF=ЁЯECM.
ЫљвдЁїMECЁеAFE(ASA)ЃЌЫљвдEC=EF.
гжвђЮЊЁЯFEC=60ЁуЃЌЫљвдЁїEFCЪЧЕШБпШ§НЧаЮ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКbЪЧзюаЁЕФе§ећЪ§ЃЌЧвaЁЂbТњзуЃЈcЉ5ЃЉ2+|a+b|=0ЃЎ
![]()
ЃЈ1ЃЉЧыЧѓГіaЁЂbЁЂcЕФжЕЃЛ
ЃЈ2ЃЉaЁЂbЁЂcЫљЖдгІЕФЕуЗжБ№ЮЊAЁЂBЁЂCЃЌЕуPЮЊвЛЖЏЕуЃЌЦфЖдгІЕФЪ§ЮЊxЃЌЕуPдк0ЕН2жЎМфдЫЖЏЪБЃЈМД0ЁмxЁм2ЪБЃЉЃЌЧыЛЏМђЪНзгЃК|x+1|-|x-1|+2|x+5|ЃЈЧыаДГіЛЏМђЙ§ГЬЃЉ
ЃЈ3ЃЉдкЃЈ1ЃЉЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуAЁЂBЁЂCПЊЪМдкЪ§жсЩЯдЫЖЏЃЌШєЕуAвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЭЌЪБЃЌЕуBКЭЕуCЗжБ№вдУПУы2ИіЕЅЮЛГЄЖШКЭ5ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдЫЖЏЃЌМйЩшtУыжгЙ§КѓЃЌШєЕуBгыЕуCжЎМфЕФОрРыБэЪОЮЊBCЃЌЕуAгыЕуBжЎМфЕФОрРыБэЪОЮЊABЃЎЧыЮЪЃКBC-ABЕФжЕЪЧЗёЫцзХЪБМфtЕФБфЛЏЖјИФБфЃПШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЃЌЧыЧѓЦфжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯACB=90ЁуЃЌDЪЧБпABЩЯвЛЕуЃЌЧвЁЯA=2ЁЯDCBЃЎEЪЧBCБпЩЯЕФвЛЕуЃЌвдECЮЊжБОЖЕФЁбOОЙ§ЕуDЃЎ
ЃЈ1ЃЉЧѓжЄЃКABЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєCDЕФЯваФОрЮЊ1ЃЌBE=EOЃЌЧѓBDЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇЩњВњЕФФГжжВњЦЗАДжЪСПЗжЮЊ10ИіЕЕДЮЃЌЕк1ЕЕДЮЃЈзюЕЭЕЕДЮЃЉЕФВњЦЗвЛЬьФмЩњВњ95МўЃЌУПМўРћШѓ6дЊЃЎУПЬсИпвЛИіЕЕДЮЃЌУПМўРћШѓдіМг2дЊЃЌЕЋвЛЬьВњСПМѕЩй5МўЃЎ
ЃЈ1ЃЉШєЩњВњЕк![]() ЕЕДЮЕФВњЦЗвЛЬьЕФзмРћШѓЮЊ
ЕЕДЮЕФВњЦЗвЛЬьЕФзмРћШѓЮЊ![]() дЊЃЈЦфжа
дЊЃЈЦфжа![]() ЮЊе§ећЪ§ЃЌЧв1Ём
ЮЊе§ећЪ§ЃЌЧв1Ём![]() Ём10ЃЉЃЌЧѓГі
Ём10ЃЉЃЌЧѓГі![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєЩњВњЕкxЕЕДЮЕФВњЦЗвЛЬьЕФзмРћШѓЮЊ1120дЊЃЌЧѓИУВњЦЗЕФжЪСПЕЕДЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
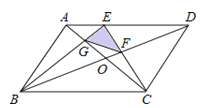
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDжаЃЌEЪЧADЩЯЕФвЛЕуЃЌЧвAE=![]() ADЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌECНЛBDгкFЃЌBEНЛACгкGЃЌШчЙћЦНааЫФБпаЮABCDЕФУцЛ§ЮЊSЃЌФЧУДЃЌЁїGEFЕФУцЛ§ЮЊЃЈ ЃЉ
ADЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌECНЛBDгкFЃЌBEНЛACгкGЃЌШчЙћЦНааЫФБпаЮABCDЕФУцЛ§ЮЊSЃЌФЧУДЃЌЁїGEFЕФУцЛ§ЮЊЃЈ ЃЉ
A. ![]() S B.
S B. ![]() S C.
S C. ![]() S D.
S D. ![]() S
S
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃзМБИЙКТђAЁЂBСНжжаЭКХРКЧђЃЌбЏЮЪСЫМзЁЂввСНМфбЇаЃСЫНтетСНПюРКЧђЕФМлИёЃЌЯТБэЪЧМзЁЂввСНМфбЇаЃЙКТђAЁЂBСНжжаЭКХРКЧђЕФЧщПіЃК
ЙКТђбЇаЃ | ЙКТђаЭКХМАЪ§СПЃЈИіЃЉ | ЙКТђжЇГіПюЯюЃЈдЊЃЉ | |
A | B | ||
Мз | 3 | 8 | 622 |
вв | 5 | 4 | 402 |
ЃЈ1ЃЉЧѓAЁЂBСНжжаЭКХЕФРКЧђЕФЯњЪлЕЅМлЃЛ
ЃЈ2ЃЉШєИУбЇаЃзМБИгУВЛЖргк1000дЊЕФН№ЖюЙКТђетСНжжаЭКХЕФРКЧђЙВ20ИіЃЌЧѓAжжаЭКХЕФРКЧђзюЩйФмВЩЙКЖрЩйИіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
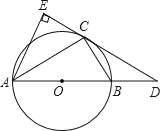
ЁОЬтФПЁПШчЭМЃЌвбжЊЁбOЪЧЁїABCЕФЭтНгдВЃЌABЪЧЁбOЕФжБОЖЃЌDЪЧABбгГЄЯпЩЯвЛЕуЃЌAEЁЭDCНЛDCЕФбгГЄЯпгкЕуEЃЌЧвACЦНЗжЁЯEABЃЎ
ЃЈ1ЃЉЧѓжЄЃКDEЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєAB=6ЃЌAE=![]() ЃЌЧѓBDКЭBCЕФГЄЃЎ
ЃЌЧѓBDКЭBCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com