
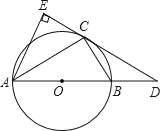
【题目】如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
(1)求证:DE是⊙O的切线;
(2)若AB=6,AE=![]() ,求BD和BC的长.
,求BD和BC的长.
【答案】(1)证明见解析;(2)BD=2;BC=![]() .
.
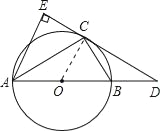
【解析】试题分析:(1)要证DE是⊙O的切线,只要连接OC,再证∠DCO=90°即可.
(2)已知两边长,求其它边的长,可以证明三角形相似,由相似三角形对应边成比例来求.
试题解析:解:(1)连接OC.∵AE⊥DC,∴∠E=90°.∵AC平分∠EAB,∴∠EAC=∠BAC.
又∵OA=OC,∴∠ACO=∠BAC,∴∠EAC=∠ACO,∴OC∥AE,∴∠OCD=∠E=90°,∴DC是⊙O的切线.
(2)∵∠D=∠D,∠E=∠OCD=90°,∴△DCO∽△DEA,∴ ![]() ,∴
,∴![]() ,∴
,∴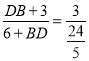 ,∴BD=2.∵AB是⊙O的直径,∴∠ACB=90°,∴∠E=∠ACB=90°.∵∠EAC=∠BAC,∴Rt△EAC∽Rt△CAB,∴
,∴BD=2.∵AB是⊙O的直径,∴∠ACB=90°,∴∠E=∠ACB=90°.∵∠EAC=∠BAC,∴Rt△EAC∽Rt△CAB,∴![]() ,∴
,∴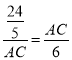 ,∴AC2=
,∴AC2=![]() .由勾股定理得:BC=
.由勾股定理得:BC=![]() =
=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:
1,-0.1,-789,25,0,-20,-3.14,![]()
正整数集{___…}; 负整数集{___…},
正分数集{____…}; 负分数集{____…};
正有理数集{______…}; 负有理数集{______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
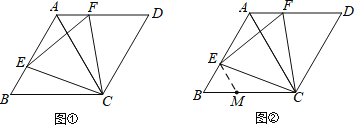
【题目】如图,在菱形ABCD中,∠B= 60°.
(1)如图①.若点E、F分别在边AB、AD上,且BE=AF,求证:△CEF是等边三角形.
(2)小明发现,当点E、F分别在边AB、AD上,且∠CEF=60°时,△CEF也是等边三角形,
并通过画图验证了猜想;小丽通过探索,认为应该以CE= EF为突破口,构造两个全等三角形:小倩受到小丽的启发,尝试在BC上截取BM =BE,并连接ME,如图②,很快就证明了△CEF是等边三角形.请你根据小倩的方法,写出完整的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
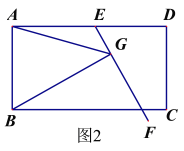
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG =AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为(1,4)的抛物线![]() 与直线
与直线![]() 交于点A(2,2),直线
交于点A(2,2),直线![]() 与
与![]() 轴交于点B与
轴交于点B与![]() 轴交于点C
轴交于点C
(1)求![]() 的值及抛物线的解析式
的值及抛物线的解析式
(2)P为抛物线上的点,点P关于直线AB的对称轴点在![]() 轴上,求点P的坐标
轴上,求点P的坐标
(3)点D为![]() 轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
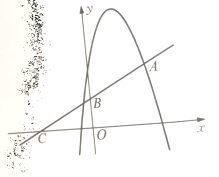
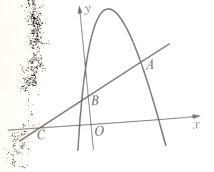
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点A(3,0),B(2,﹣3),并且以x=1为对称轴.
(1)求此函数的解析式;
(2)作出二次函数的大致图象;
(3)在对称轴x=1上是否存在一点P,使△PAB中PA=PB?若存在,求出P点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面的材料,完成有关问题:
材料:在学习绝对值时,我们已了解绝对值的几何意义,如|5-3|表示5、3在数轴上对应的两点之间的距离;又如|5+3|=|5-(-3)|,所以|5+3|表示5、-3在数轴上对应的两点之间的距离。因此,一般地,点A,B在数轴上分别表示有理数a,b,那么A,B之间的距离(也就是线段AB的长度)可表示为|a-b|。
因此我们可以用绝对值的几何意义按如下方法求![]() 的最小值;
的最小值;
![]() 即数轴上x与1对应的点之间的距离,
即数轴上x与1对应的点之间的距离,![]() 即数轴上x与2对应的点之间的距离,把这两个距离在同一个数轴上表示出来,然后把距离相加即可得原式的值.
即数轴上x与2对应的点之间的距离,把这两个距离在同一个数轴上表示出来,然后把距离相加即可得原式的值.
设A、B、P三点对应的数分别是1、2、x.
当1≤x≤2时,即P点在线段AB上,此时![]() ;
;
当x>2时,即P点在B点右侧,此时![]() = PA+PB=AB+2PB>AB;
= PA+PB=AB+2PB>AB;
当x <1时,即P点在A点左侧,此时![]() =PA+PB=AB+2PA>AB;
=PA+PB=AB+2PA>AB;
综上可知,当1≤x≤2时(P点在线段AB上),![]() 取得最小值为1.
取得最小值为1.
![]()
![]()
![]()
请你用上面的思考方法结合数轴完成以下问题:
(1)满足![]() 的x的取值范围是 。
的x的取值范围是 。
(2)求![]() 的最小值为 ,最大值为 。
的最小值为 ,最大值为 。
备用图:
![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com