
【题目】已知:b是最小的正整数,且a、b满足(c﹣5)2+|a+b|=0.
![]()
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子:|x+1|-|x-1|+2|x+5|(请写出化简过程)
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
【答案】(1)-1;1;5;(2)4x+10或2x+12.;(3)不变,理由见解析.
【解析】
(1)根据b是最小的正整数,即可确定b的值,然后根据非负数的性质,几个非负数的和是0,则每个数是0,即可求得a,b,c的值;
(2)根据x的范围,确定x+1,x-3,5-x的符号,然后根据绝对值的意义即可化简;
(3)先求出BC=3t+4,AB=3t+2,从而得出BC-AB=2.
(1)∵b是最小的正整数,∴b=1.
根据题意得:c-5=0且a+b=0,
∴a=-1,b=1,c=5.
故答案是:-1;1;5;
(2)当0≤x≤1时,x+1>0,x-1≤0,x+5>0,
则:|x+1|-|x-1|+2|x+5|
=x+1-(1-x)+2(x+5)
=x+1-1+x+2x+10
=4x+10;
当1<x≤2时,x+1>0,x-1>0,x+5>0.
∴|x+1|-|x-1|+2|x+5|=x+1-(x-1)+2(x+5)
=x+1-x+1+2x+10
=2x+12;
(3)不变.理由如下:
t秒时,点A对应的数为-1-t,点B对应的数为2t+1,点C对应的数为5t+5.
∴BC=(5t+5)-(2t+1)=3t+4,AB=(2t+1)-(-1-t)=3t+2,
∴BC-AB=(3t+4)-(3t+2)=2,
即BC-AB的不随着时间t的变化而改变.


科目:初中数学 来源: 题型:
【题目】(1)15-[3-(-5-4)];
(2)2.5-(-2)÷![]() -1.5;
-1.5;
(3)2-{8+(-1)-[(-4)×2÷(-2)+6×(-6)]}.
(4)(-5)×(+2019)+(+7)×(-2019)+12×2019.
(5)![]() (用简便方法).
(用简便方法).
(6)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC中,∠BAC=90°,AD⊥BC于点D,AB=5,点E是边AB上的动点(不与A,B点重合),连接DE,过点D作DF⊥DE交AC于点F,连接EF,点H在线段AD上,且DH=![]() AD,连接EH,HF,记图中阴影部分的面积为S1,△EHF的面积记为S2,则S2的取值范围是_______.
AD,连接EH,HF,记图中阴影部分的面积为S1,△EHF的面积记为S2,则S2的取值范围是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图,求∠QEP的度数;
(2)如图,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆节放假时,小华一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆.早上从家里出发,向东走了4千米到超市买东西,然后又向东走了3千米到爷爷家,中午从爷爷家出发向西走了12千米到外公家,晚上返回家里.
(1)若以家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来;
(2)问超市A和外公家C相距多少千米?
(3)若小轿车每千米耗油0.09升,求小明一家从出发到返回家所经历路程小车的耗油量.(精确到0.1升)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点![]() 对应的数分别是
对应的数分别是![]() 、
、![]() ,
,![]() 为数轴上两个动点,它们同时向右运动.点
为数轴上两个动点,它们同时向右运动.点![]() 从点
从点![]() 出发,速度为每秒
出发,速度为每秒![]() 个单位长度;点
个单位长度;点![]() 从点
从点![]() 出发,速度为点
出发,速度为点![]() 的
的![]() 倍,点
倍,点![]() 为原点.
为原点.
(1)当运动![]() 秒时,点
秒时,点![]() 对应的数分别是 、 .
对应的数分别是 、 .
(2)求运动多少秒时,点![]() 中恰有一个点为另外两个点所连线段的中点?
中恰有一个点为另外两个点所连线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .
(2)数轴上表示﹣12和﹣6的两点之间的距离是 .
(3)数轴上表示x和1的两点之间的距离表示为 .
(4)若x表示一个有理数,且﹣4<x<2,则|x﹣2|+|x+4|= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:
1,-0.1,-789,25,0,-20,-3.14,![]()
正整数集{___…}; 负整数集{___…},
正分数集{____…}; 负分数集{____…};
正有理数集{______…}; 负有理数集{______…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
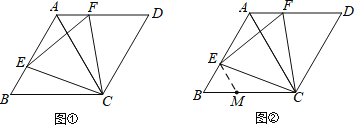
【题目】如图,在菱形ABCD中,∠B= 60°.
(1)如图①.若点E、F分别在边AB、AD上,且BE=AF,求证:△CEF是等边三角形.
(2)小明发现,当点E、F分别在边AB、AD上,且∠CEF=60°时,△CEF也是等边三角形,
并通过画图验证了猜想;小丽通过探索,认为应该以CE= EF为突破口,构造两个全等三角形:小倩受到小丽的启发,尝试在BC上截取BM =BE,并连接ME,如图②,很快就证明了△CEF是等边三角形.请你根据小倩的方法,写出完整的证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com