
【题目】如图,已知等腰直角△ABC中,∠BAC=90°,AD⊥BC于点D,AB=5,点E是边AB上的动点(不与A,B点重合),连接DE,过点D作DF⊥DE交AC于点F,连接EF,点H在线段AD上,且DH=![]() AD,连接EH,HF,记图中阴影部分的面积为S1,△EHF的面积记为S2,则S2的取值范围是_______.
AD,连接EH,HF,记图中阴影部分的面积为S1,△EHF的面积记为S2,则S2的取值范围是_______.

【答案】![]() ≤S2<
≤S2<![]()
【解析】
作EM⊥BC于M,作FN⊥AD于N,根据题意可证△ADF≌△BED,可得△DFE是等腰直角三角形.可证△BME≌△ANF,可得NF=BM.所以S1=![]() HD×BD,代入可求S1,由点E是边AB上的动点(不与A,B点重合),可得DE垂直AB时DE最小,即
HD×BD,代入可求S1,由点E是边AB上的动点(不与A,B点重合),可得DE垂直AB时DE最小,即![]() ≤DE<
≤DE<![]() ,且S2=S△DEF-S1,代入可求S2的取值范围
,且S2=S△DEF-S1,代入可求S2的取值范围
解:作EM⊥BC于M,作FN⊥AD于N,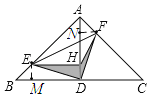
∵EM⊥BD,AD⊥BC
∴EM∥AD
∵△ABC是等腰直角三角形,AD⊥BC,AB=5
∴∠B=∠C=45°=∠BAD=∠DAC,BD=CD=AD=![]()
∵DF⊥DE
∴∠ADF+∠ADE=90°且∠ADE+∠BDE=90°
∴∠ADF=∠BDE且AD=BD,∠B=∠DAF=45°
∴△ADF≌△BDE,
∴AF=BE,DE=DF
∴△DEF是等腰直角三角形,
∵AF=BE,∠B=∠DAF=45°,∠EMB=∠ANF=90°
∴△BME≌△ANF
∴NF=BM
∵S1=S△EHD+S△DHF=![]() HD×MD+
HD×MD+![]() HD×FN=
HD×FN=![]() ×
×![]() AD×(BM+MD)=
AD×(BM+MD)=![]() AD2=
AD2=![]()
∵点E是边AB上的动点
∴![]() ≤DE<
≤DE<![]() ,
,
∵S2=S△DEF-S1=![]() DE2-
DE2-![]()
∴![]() ≤S2<
≤S2<![]()
故答案为:![]() ≤S2<
≤S2<![]() .
.


科目:初中数学 来源: 题型:
【题目】点A,B,C为数轴上的三点,如果点C在点A,B之间,且到点A的距离是点C到点B的距离的3倍,那么我们就称点C是{A,B}的奇妙点.例如,如图①,点A表示的数为-3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇妙点;又如,表示-2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇妙点.
(知识运用)
如图②,M,N为数轴上的两点,点M所表示的数为-2,点N所表示的数为6.
(1)表示数_____的点是{M,N}的奇妙点;表示数______的点是{N,M}的奇妙点;
(2)若点P所表示的数为3,点P是{M,N}的奇妙点,则点M、N所表示的数可以是几?M=______,N=_____(写出一组即可)
(3)如图③,A,B为数轴上的两点,点A所表示的数为-10,点B所表示的数为50.现有一动点P从点A出发向右运动,点P运动到数轴上的什么位置时,P,A,B中恰有一个点为其余两点的奇妙点?

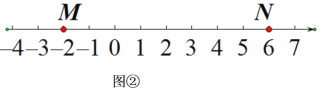
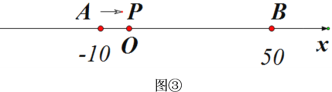
查看答案和解析>>
科目:初中数学 来源: 题型:
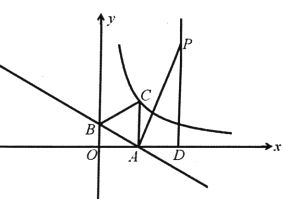
【题目】如图,一次函数y=-![]() x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y=![]() 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;
(2)点P(2![]() ,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为鼓励创业,某市政府制定了小型企业的优惠政策,许多小型企业应运而生,某社区统计了该社区今年1~6月份新注册小型企业的数量,并将结果绘制成如下的条形统计图和扇形统计图:
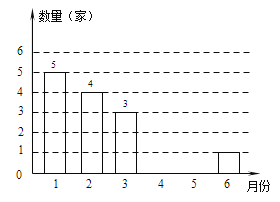

根据以上信息解答下列问题:
(1)该社区1~6月新注册小型企业一共有__________家;
(2)补全条形统计图。
(3)扇形统计图中“4月份”所在扇形的圆心角的度数为 ;
(4)如果该市今年1~6月份新注册小型企业共有1200家,估计全市今年1月份新注册小型企业的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区计划对面积为1600m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,规定甲乙两队单独施工的总天数不超过25天完成,且施工总费用最低,则最低费用为__________万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区积极开展“体育大课间”活动,引导学生坚持体育锻炼,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步.D:足球四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调査,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题:
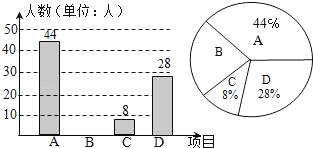
(1)求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数;
(2)请把条形统计图补充完整;
(3)己知该校有2000人,请根据样本估计全校最喜欢足球的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
(1)(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
(2)(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足(c﹣5)2+|a+b|=0.
![]()
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子:|x+1|-|x-1|+2|x+5|(请写出化简过程)
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com