
【题目】我区积极开展“体育大课间”活动,引导学生坚持体育锻炼,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步.D:足球四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调査,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题:
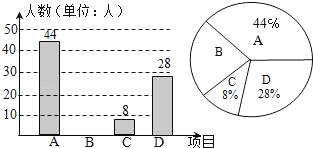
(1)求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数;
(2)请把条形统计图补充完整;
(3)己知该校有2000人,请根据样本估计全校最喜欢足球的人数是多少?
【答案】(1)20%,72°;(2)补图见解析;(3)560人.
【解析】
试题分析:(1)用整体1减去A,C、D所占的百分比,即可求出B所占的百分比,再用B所占的百分比乘以360°即可得出答案;
(2)根据C所占的百分比与所给的人数,求出总人数,再用总人数乘以B所占的百分比,从而补全图形;
(3)根据D所占的百分比乘以总人数即可得出全校最喜欢足球的人数.
试题解析:(1)样本中最喜欢B项目的人数百分比是1-44%-28%-8%=20%,
其所在扇形图中的圆心角的度数是20%×360°=72°;
(2)总人数是8÷8%=100(人),
B的人数是:100×20%=20(人),
如图:
 ;
;
(3)根据题意得:
2000×28%=560(人),
答:全校最喜欢足球的人数是560人.


科目:初中数学 来源: 题型:
【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{A,B}的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,当P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(-2,1),B(-3,-2),C(1,-2).把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
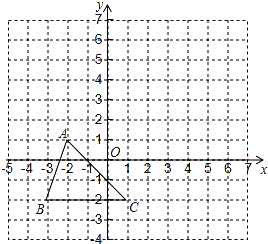
(1)在图中画出△A′B′C′,并写出点A′,B′,C′的坐标;
(2)连接A′C和A′A,求三角形AA′C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC中,∠BAC=90°,AD⊥BC于点D,AB=5,点E是边AB上的动点(不与A,B点重合),连接DE,过点D作DF⊥DE交AC于点F,连接EF,点H在线段AD上,且DH=![]() AD,连接EH,HF,记图中阴影部分的面积为S1,△EHF的面积记为S2,则S2的取值范围是_______.
AD,连接EH,HF,记图中阴影部分的面积为S1,△EHF的面积记为S2,则S2的取值范围是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=![]() ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图,求∠QEP的度数;
(2)如图,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点![]() 对应的数分别是
对应的数分别是![]() 、
、![]() ,
,![]() 为数轴上两个动点,它们同时向右运动.点
为数轴上两个动点,它们同时向右运动.点![]() 从点
从点![]() 出发,速度为每秒
出发,速度为每秒![]() 个单位长度;点
个单位长度;点![]() 从点
从点![]() 出发,速度为点
出发,速度为点![]() 的
的![]() 倍,点
倍,点![]() 为原点.
为原点.
(1)当运动![]() 秒时,点
秒时,点![]() 对应的数分别是 、 .
对应的数分别是 、 .
(2)求运动多少秒时,点![]() 中恰有一个点为另外两个点所连线段的中点?
中恰有一个点为另外两个点所连线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1:![]() .
.

(1)求加固后坝底增加的宽度AF;
(2)求完成这项工程需要土石多少立方米?(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com