
【题目】如图,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图,求∠QEP的度数;
(2)如图,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.

【答案】(1)60°,理由见解析;(2)BQ=2![]() ﹣2
﹣2![]() .
.
【解析】
(1)先证明出△CQB≌△CPA,即可得出∠QEP=60°;
(2)作CH⊥AD于H,如图2,证明△ACP≌△BCQ,则AP=BQ,由∠DAC=135°,∠ACP=15°,得出AH=3,CH=3![]() ,即可得出PH=CH=3
,即可得出PH=CH=3![]() ,即可得出结论.
,即可得出结论.
(1)如图1,∵PC=CQ,且∠PCQ=60°,则△CQB和△CPA中,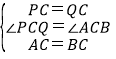 ,∴△CQB≌△CPA(SAS),
,∴△CQB≌△CPA(SAS),
∴∠CQB=∠CPA,又因为△PEM和△CQM中,∠EMP=∠CMQ, ∴∠QEP=∠QCP=60°.
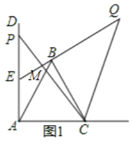
(2)作CH⊥AD于H,如图2,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵线段CP绕点C顺时针旋转60°得到线段CQ,
∴CP=CQ,∠PCQ=6O°,
∴∠ACB+∠BCP=∠BCP+∠PCQ,
即∠ACP=∠BCQ,
在△ACP和△BCQ中,
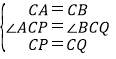
∴△ACP≌△BCQ(SAS),
∴AP=BQ,
∵∠DAC=135°,∠ACP=15°,∴∠APC=30°,∠PCB=45°,∴△ACH为等腰直角三角形,
∴AH=CH=![]() AC=
AC=![]() ×4=2
×4=2![]() ,在Rt△PHC中,PH=
,在Rt△PHC中,PH=![]() CH=2
CH=2![]() ,∴PA=PH﹣AH=2
,∴PA=PH﹣AH=2![]() ﹣2
﹣2![]() ,
,
∴BQ=2![]() ﹣2
﹣2![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为_________cm.

(第16题图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为鼓励创业,某市政府制定了小型企业的优惠政策,许多小型企业应运而生,某社区统计了该社区今年1~6月份新注册小型企业的数量,并将结果绘制成如下的条形统计图和扇形统计图:
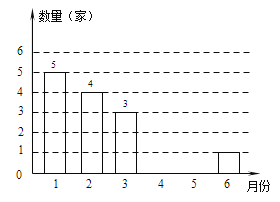

根据以上信息解答下列问题:
(1)该社区1~6月新注册小型企业一共有__________家;
(2)补全条形统计图。
(3)扇形统计图中“4月份”所在扇形的圆心角的度数为 ;
(4)如果该市今年1~6月份新注册小型企业共有1200家,估计全市今年1月份新注册小型企业的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区积极开展“体育大课间”活动,引导学生坚持体育锻炼,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步.D:足球四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调査,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题:
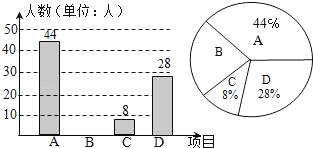
(1)求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数;
(2)请把条形统计图补充完整;
(3)己知该校有2000人,请根据样本估计全校最喜欢足球的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
(1)(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
(2)(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个几何体由大小相同的正方体搭成,从上面看到的几何体的形的形状状图如图所示,其中小正方形中的数字表示在该位置的小正方体的个数,

(1)请画出从正面和左面看到的这个几何体的形状图.
(2)若每个小正方图的棱长都为1,则搭成的这个几何体的体积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足(c﹣5)2+|a+b|=0.
![]()
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子:|x+1|-|x-1|+2|x+5|(请写出化简过程)
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
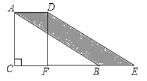
【题目】如图,在RtΔABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB方向向右平移得到△DEF.若四边形ABED的面积为8,则平移距离为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第![]() 档次的产品一天的总利润为
档次的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且1≤
为正整数,且1≤![]() ≤10),求出
≤10),求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com