练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

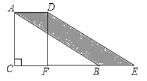
    【题目】如图，在RtΔABC中，∠C=90°，∠ABC=30°，AB=8,将△ABC沿CB方向向右平移得到△DEF.若四边形ABED的面积为8，则平移距离为__.

    【答案】2.

    【解析】

    先根据含30度的直角三角形三边的关系得到AC=AB=4，再根据平移的性质得AD=BE，AD∥BE，于是可判断四边形ABED为平行四边形，则根据平行四边形的面积公式得到ACBE=8，即4BE=8，则可计算出BE=2，所以平移距离等于2．

    在Rt△ABC中，∵∠ABC=30°，

    ∴AC=AB=4，

    ∵△ABC沿CB向右平移得到△DEF，

    ∴AD=BE，AD∥BE，

    ∴四边形ABED为平行四边形，

    ∵四边形ABED的面积等于8，

    ∴ACBE=8，即4BE=8，

    ∴BE=2，
    即平移距离等于2．

    故答案为：2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的顶点坐标分别为A（-2,1），B（-3,-2），C（1，-2）.把△ABC向上平移4个单位长度，再向右平移3个单位长度，得到△A′B′C′．

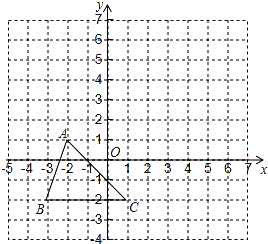
    （1）在图中画出△A′B′C′，并写出点A′，B′，C′的坐标；

    （2）连接A′C和A′A，求三角形AA′C的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠DAC＝90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连结CP，将线段CP绕点C顺时针旋转60°得到线段CQ，连结QB并延长交直线AD于点E．

    （1）如图，求∠QEP的度数；

    （2）如图，若∠DAC＝135°，∠ACP＝15°，且AC＝4，求BQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数轴上点对应的数分别是、，为数轴上两个动点，它们同时向右运动.点从点出发，速度为每秒个单位长度；点从点出发，速度为点的倍，点为原点.

    （1）当运动秒时，点对应的数分别是 、 .

    （2）求运动多少秒时，点中恰有一个点为另外两个点所连线段的中点？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB＝|a﹣b|．

    利用数形结合思想回答下列问题：

    (1)数轴上表示1和3两点之间的距离　 　．

    (2)数轴上表示﹣12和﹣6的两点之间的距离是　 　．

    (3)数轴上表示x和1的两点之间的距离表示为　 　．

    (4)若x表示一个有理数，且﹣4＜x＜2，则|x﹣2|+|x+4|＝　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

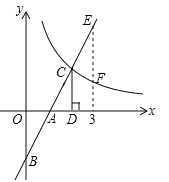
    【题目】（3分）如图，在直角坐标系中，直线与坐标轴交于A、B两点，与双曲线（）交于点C，过点C作CD⊥x轴，垂足为D，且OA=AD，则以下结论：

    ①；

    ②当0＜x＜3时，；

    ③如图，当x=3时，EF=；

    ④当x＞0时，随x的增大而增大，随x的增大而减小．

    其中正确结论的个数是（ ）

    A．1 B．2 C．3 D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把下列各数填在相应的大括号内：

    1，-0.1，-789，25，0，-20，-3.14，

    正整数集{___…}； 负整数集{___…}，

    正分数集{____…}； 负分数集{____…}；

    正有理数集{______…}； 负有理数集{______…}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某防洪指挥部发现长江边一处长500米，高10米，背水坡的坡角为45°的防洪大堤（横断面为梯形ABCD）急需加固．经调查论证，防洪指挥部专家组制定的加固方案是：背水坡面用土石进行加固，并使上底加宽3米，加固后背水坡EF的坡比i=1：．

    （1）求加固后坝底增加的宽度AF；

    （2）求完成这项工程需要土石多少立方米？（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

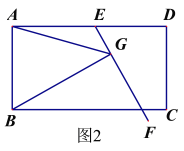
    问题：如图1，在平行四边形ABCD中，E是AD上一点，AE=AB，∠EAB=60°，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG.

    求证：EG =AG+BG.

    小明同学的思路是：作∠GAH=∠EAB交GE于点H，构造全等三角形，经过推理解决问题.

    参考小明同学的思路，探究并解决下列问题：

    （1）完成上面问题中的证明；

    （2）如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”，原问题中的其它条件不变（如图2），请探究线段EG、AG、BG之间的数量关系，并证明你的结论.

    查看答案和解析>>

    同步练习册答案