
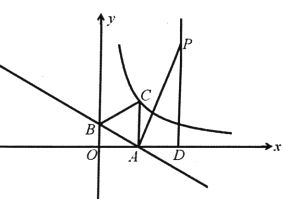
【题目】如图,一次函数y=-![]() x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y=![]() 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;
(2)点P(2![]() ,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
【答案】![]()
![]() ;
; ![]() P点坐标为
P点坐标为![]()
【解析】试题分析:(1)由直线解析式可求得A、B坐标,在Rt△AOB中,利用三角函数定义可求得∠BAO=30°,且可求得AB的长,从而可求得CA⊥OA,则可求得C点坐标,利用待定系数法可求得反比例函数解析式;
(2)分△PAD∽△ABO和△PAD∽△BAO两种情况,分别利用相似三角形的性质可求得m的值,可求得P点坐标,代入反比例函数解析式进行验证即可.
试题解析:解:(1)在![]() 中,令y=0可解得x=
中,令y=0可解得x=![]() ,令x=0可得y=1,∴A(
,令x=0可得y=1,∴A(![]() ,0),B(0,1),∴tan∠BAO=
,0),B(0,1),∴tan∠BAO=![]() ,∴∠BAO=30°,∵△ABC是等边三角形,∴∠BAC=60°,∴∠CAO=90°,在Rt△BOA中,由勾股定理可得AB=2,∴AC=2,∴C(
,∴∠BAO=30°,∵△ABC是等边三角形,∴∠BAC=60°,∴∠CAO=90°,在Rt△BOA中,由勾股定理可得AB=2,∴AC=2,∴C(![]() ,2),∵点C在反比例函数
,2),∵点C在反比例函数![]() 的图象上,∴k=2×
的图象上,∴k=2×![]() =
=![]() ,∴反比例函数解析式为
,∴反比例函数解析式为![]() ;
;
(2)∵P(![]() ,m)在第一象限,∴AD=OD﹣OA=
,m)在第一象限,∴AD=OD﹣OA=![]() ﹣
﹣![]() =
=![]() ,PD=m,当△ADP∽△AOB时,则有
,PD=m,当△ADP∽△AOB时,则有![]() ,即
,即![]() ,解得m=1,此时P点坐标为(
,解得m=1,此时P点坐标为(![]() ,1);
,1);
当△PDA∽△AOB时,则有![]() ,即
,即![]() ,解得m=3,此时P点坐标为(
,解得m=3,此时P点坐标为(![]() ,3);
,3);
把P(![]() ,3)代入
,3)代入![]() 可得3≠
可得3≠![]() ,∴P(
,∴P(![]() ,3)不在反比例函数图象上,把P(
,3)不在反比例函数图象上,把P(![]() ,1)代入反比例函数解析式得1=
,1)代入反比例函数解析式得1=![]() ,∴P(
,∴P(![]() ,1)在反比例函数图象上;
,1)在反比例函数图象上;
综上可知P点坐标为(![]() ,1).
,1).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
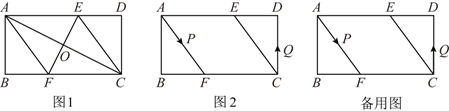
(1)如图1,连接AF、CE求证:四边形AFCE为菱形;
(2)如图1,求AF的长;
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:克) | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)若每袋食品的标准质量为450克,则抽样检测的20袋食品的总质量是多少克?
(2)若该种食品的合格标准为450±5克,求该种食品抽样检测的合格率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)15-[3-(-5-4)];
(2)2.5-(-2)÷![]() -1.5;
-1.5;
(3)2-{8+(-1)-[(-4)×2÷(-2)+6×(-6)]}.
(4)(-5)×(+2019)+(+7)×(-2019)+12×2019.
(5)![]() (用简便方法).
(用简便方法).
(6)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
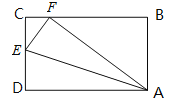
【题目】如图,四边形ABCD是矩形纸片,AD=10,CD=8,在CD边上取一点E,将纸片沿AE折叠,使点D落在BC边上的F处.
(1)AF的长=_____.
(2)BF的长=______.
(3)CF的长=_____.
(4)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(-2,1),B(-3,-2),C(1,-2).把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
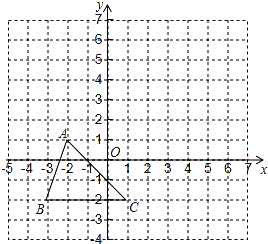
(1)在图中画出△A′B′C′,并写出点A′,B′,C′的坐标;
(2)连接A′C和A′A,求三角形AA′C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
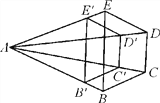
(1)求证:四边形BCDE位似于四边形B′C′D′E′;
(2)若![]() =3,S四边形BCDE=20,求S四边形B′C′D′E′.
=3,S四边形BCDE=20,求S四边形B′C′D′E′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC中,∠BAC=90°,AD⊥BC于点D,AB=5,点E是边AB上的动点(不与A,B点重合),连接DE,过点D作DF⊥DE交AC于点F,连接EF,点H在线段AD上,且DH=![]() AD,连接EH,HF,记图中阴影部分的面积为S1,△EHF的面积记为S2,则S2的取值范围是_______.
AD,连接EH,HF,记图中阴影部分的面积为S1,△EHF的面积记为S2,则S2的取值范围是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .
(2)数轴上表示﹣12和﹣6的两点之间的距离是 .
(3)数轴上表示x和1的两点之间的距离表示为 .
(4)若x表示一个有理数,且﹣4<x<2,则|x﹣2|+|x+4|= .
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com