
����Ŀ����֪������ABCD�У�AB=4cm��BC=8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO��
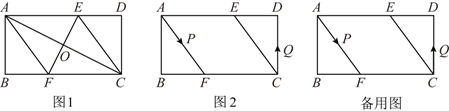
(1)��ͼ1������AF��CE��֤���ı���AFCEΪ���Σ�
(2)��ͼ1����AF�ij���
(3)��ͼ2������P��Q�ֱ��A��C����ͬʱ�������ء�AFB�͡�CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У���P���ٶ�Ϊÿ��1cm�����˶�ʱ��Ϊt�룮����Q���ٶ�Ϊÿ��0.8cm����A��P��C��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��
���𰸡���1������������2��AF=5cm����3��![]()
��������
��1�����ݾ��ε����ʡ�ƽ���ߵ����ʺ���֪��������ASA֤����AOE�ա�COF���ɵ�OE=OF�������ɵ��ı���AFCE��ƽ���ı��Σ�Ȼ����EF��AC����֤�ý��ۣ�
��2����AF=xcm������CF=xcm��BF=(8��x)cm��Ȼ����Rt��ABF�У��ɹ��ɶ�����������x�ķ��̣��ⷽ�̼��ý����
��3����Ϊ�����������һ��P��AF�ϣ���P��Q������ٶȼ��ɽ����жϣ��ڶ�����P��BF��ʱ��Q��CD��DE�ϣ�����ֻ�е�Q��DE��ʱ����A��P��C��Q�ĵ�Ϊ������ı��β��п�����ƽ���ı��Σ���ͼ���ú�t�Ĵ���ʽ�ֱ��ʾ��AQ��CP���Ӷ��ɵù���t�ķ��̣��ⷽ�̼��ý���������������P��AB��ʱ��Q��DE��CE�ϣ���P��Q�����λ�ü��ɽ����жϣ�
(1)֤�������ı���ABCD�Ǿ��Σ�
��AD��BC��
���EAO=��FCO��
��EF��AC�Ĵ�ֱƽ���ߣ�
��OA=OC��
�ߡ�AOE=��COF��
����AOE����COF��ASA����
��OE=OF��
��OA=OC��
���ı���AFCE��ƽ���ı��Σ�
��EF��AC��
��ƽ���ı���AFCE�����Σ�
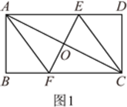
��2�����ı���AFCE�����Σ�
��AF=FC��
��AF=xcm����CF=xcm��BF=(8��x)cm��
���ı���ABCD�Ǿ��Σ����B=90����
����Rt��ABF�У��ɹ��ɶ����ã�![]() ��
��
��ã�x=5����AF=5cm��
(3)�����������
��һ��P��AF�ϣ���P���ٶ���1cm/s����Q���ٶ���0.8cm/s��
��Qֻ����CD�ϣ���ʱ��A��P��C��Q�ĵ�Ϊ������ı��β���ƽ���ı��Σ�
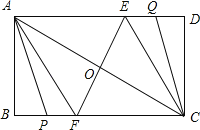
�ڶ�����P��BF��ʱ��Q��CD��DE�ϣ�����ֻ�е�Q��DE��ʱ����A��P��C��Q�ĵ�Ϊ������ı��β��п�����ƽ���ı��Σ���ͼ��
��AQ=8��(0.8t��4)��CP=5+(t��5)��
��8��(0.8t��4)=5+(t��5)��
��ã�![]() ��
��
�����������P��AB��ʱ��Q��DE��CE�ϣ���ʱ��A��P��C��Q�ĵ�Ϊ������ı��β���ƽ���ı��Σ�
������������![]() ʱ����A��P��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
ʱ����A��P��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,��OΪ����ԭ��,AB![]() OC,��B,C������ֱ�Ϊ��15,8��,��21,0��,����M�ӵ�A��A��B��ÿ��1����λ���ٶ��˶�;����N�ӵ�C��C��O��ÿ��2����λ���ٶ��˶���M,Nͬʱ����,���˶�ʱ��Ϊt�룮
OC,��B,C������ֱ�Ϊ��15,8��,��21,0��,����M�ӵ�A��A��B��ÿ��1����λ���ٶ��˶�;����N�ӵ�C��C��O��ÿ��2����λ���ٶ��˶���M,Nͬʱ����,���˶�ʱ��Ϊt�룮
��1����t��3ʱ,M�������� ��,N�������� ��;
��2����tΪ��ֵʱ,�ı���OAMN�Ǿ��Σ�
��3���˶�������,�ı���MNCB�ܷ�Ϊ���Σ�����,���t��ֵ;������,˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��![]() �������� ��2����5.6+0.9��4.4+8.1��0.1
�������� ��2����5.6+0.9��4.4+8.1��0.1
��3��![]() ���������� ��4��
���������� ��4��![]()
��5��![]() �������� ��6��
�������� ��6��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и��������������ļ����ڣ������и���������Ӧ�������ڣ�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����
�������ϣ�{ ��}��
�������ϣ�{ ��}��
���������ϣ�{ ��}��
�����������ϣ�{ ��}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1�������ɸ�СԲȦ�ѳɵ�һ������ȱ������ε�ͼ����������һ����һ��ԲȦ��
���¸��������һ���һ��ԲȦ��һ������n �㣮��ͼ1���ú���ԭͼ1ƴ��ͼ2����״���������ǿ���
���ͼ1������ԲȦ�ĸ���Ϊ1��2��3������n��![]() ��
��

���ͼ�е�ԲȦ����13�㣬�����������⣺
��1�������������£���ÿ��ԲȦ�а�ͼ3�ķ�ʽ����һ��������������1��2��3��4������������ײ�����
�����ԲȦ�е����� ��
��2�������������£���ÿ��ԲȦ�а�ͼ4�ķ�ʽ����һ��������������23����22����21����20����������
��ײ����ұ�ԲȦ�ڵ�����_______��
��3����ͼ4������ԲȦ�и����ľ���ֵ֮�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ�������ڼ���![]() Ԫ����
Ԫ����![]() ���ֿ���
���ֿ���![]() ��������
��������![]() �ֿ����빺��
�ֿ����빺��![]() �ֿ��ֵķ�����ͬ����
�ֿ��ֵķ�����ͬ����![]() �ֿ��ֵĵ�����
�ֿ��ֵĵ�����![]() �ֿ��ֵ��۵�
�ֿ��ֵ��۵�![]() ��.
��.
![]() ��
��![]() ���ֿ��ֵĵ��۸��Ƕ���Ԫ��
���ֿ��ֵĵ��۸��Ƕ���Ԫ��
![]() ���ƻ��ò�����
���ƻ��ò�����![]() Ԫ���ʽ��ٴι���
Ԫ���ʽ��ٴι���![]() ���ֿ��ֹ�
���ֿ��ֹ�![]() ������֪
������֪![]() ���ֿ��ֵĽ��۲��䣬��
���ֿ��ֵĽ��۲��䣬��![]() �ֿ�������ܹ�����ٸ���
�ֿ�������ܹ�����ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������Ƥ�����ĸ��Ǹ���ȥһ���߳�Ϊ2�������κ�ʣ�µIJ�������һ���ݻ�Ϊ90�������dz��������ӣ���֪���������ӵ���ij��ȿ���4�ף��������Ƥ�������
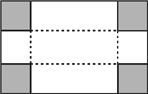
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B��CΪ�����ϵ����㣬�����C�ڵ�A��B֮�䣬�ҵ���A�ľ����ǵ�C����B�ľ����3������ô���ǾͳƵ�C��{A��B}������㣮���磬��ͼ�٣���A��ʾ����Ϊ��3����B��ʾ����Ϊ1.��ʾ0�ĵ�C����A�ľ�����3������B�ľ�����1����ô��C��{A��B}������㣻���磬��ʾ��2�ĵ�D����A�ľ�����1������B�ľ�����3����ô��D�Ͳ���{A��B}����㣬����D��{B��A}������㣮
��֪ʶ���ã�
��ͼ�ڣ�M��NΪ�����ϵ����㣬��M����ʾ����Ϊ��2����N����ʾ����Ϊ6.
(1)��ʾ��_____�ĵ���{M��N}������㣻��ʾ��______�ĵ���{N��M}������㣻
(2)����P����ʾ����Ϊ3����P��{M��N}������㣬���M��N����ʾ���������Ǽ���M=______��N=_____(д��һ�鼴��)
(3)��ͼ�ۣ�A��BΪ�����ϵ����㣬��A����ʾ����Ϊ��10����B����ʾ����Ϊ50.����һ����P�ӵ�A���������˶�����P�˶��������ϵ�ʲôλ��ʱ��P��A��B��ǡ��һ����Ϊ�������������㣿

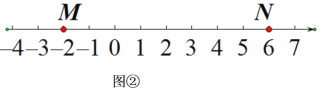
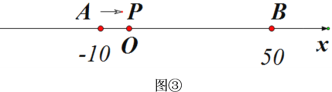
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
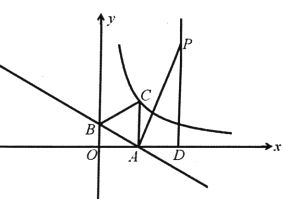
����Ŀ����ͼ��һ�κ���y����![]() x��1��ͼ����x�ᡢy��ֱ��ڵ�A��B�����߶�ABΪ���ڵ�һ�������ȱߡ�ABC.
x��1��ͼ����x�ᡢy��ֱ��ڵ�A��B�����߶�ABΪ���ڵ�һ�������ȱߡ�ABC.
(1)����C�ڷ���������y��![]() ��ͼ���ϣ���÷����������Ľ���ʽ��
��ͼ���ϣ���÷����������Ľ���ʽ��
(2)��P(2![]() ��m)�ڵ�һ���ޣ�����P��x��Ĵ��ߣ�����ΪD������PAD���OAB����ʱ��P���Ƿ���(1)�з���������ͼ���ϣ�����ڣ����P�����ꣻ������ڣ������˵��.
��m)�ڵ�һ���ޣ�����P��x��Ĵ��ߣ�����ΪD������PAD���OAB����ʱ��P���Ƿ���(1)�з���������ͼ���ϣ�����ڣ����P�����ꣻ������ڣ������˵��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com