
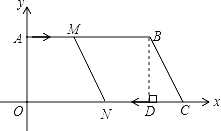
【题目】如图,在平面直角坐标系中,点O为坐标原点,AB![]() OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.
OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.
(1)在t=3时,M点坐标 ,N点坐标 ;
(2)当t为何值时,四边形OAMN是矩形?
(3)运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.

【答案】(1)(3,8);(15,0);(2)t=7;(3)能,t=5.
【解析】
(1)根据点B、C的坐标求出AB、OA、OC,然后根据路程=速度×时间求出AM、CN,再求出ON,然后写出点M、N的坐标即可;
(2)根据有一个角是直角的平行四边形是矩形,当AM=ON时,四边形OAMN是矩形,然后列出方程求解即可;
(3)先求出四边形MNCB是平行四边形的t值,并求出CN的长度,然后过点B作BC⊥OC于D,得到四边形OABD是矩形,根据矩形的对边相等可得OD=AB,BD=OA,然后求出CD,再利用勾股定理列式求出BC,然后根据邻边相等的平行四边形是菱形进行验证.
解:(1)∵B(15,8),C(21,0),
∴AB=15,OA=8,
OC=21,
当t=3时,AM=1×3=3,
CN=2×3=6,
∴ON=OC-CN=21﹣6=15,
∴点M(3,8),N(15,0);
故答案为:(3,8);(15,0);
(2)当四边形OAMN是矩形时,AM=ON,
∴t=21-2t,
解得t=7秒,
故t=7秒时,四边形OAMN是矩形;
(3)存在t=5秒时,四边形MNCB能否为菱形.
理由如下:四边形MNCB是平行四边形时,BM=CN,
∴15-t=2t,
解得:t=5秒,
此时CN=5×2=10,
过点B作BD⊥OC于D,则四边形OABD是矩形,
∴OD=AB=15,BD=OA=8,
CD=OC-OD=21-15=6,
在Rt△BCD中,BC=![]() =10,
=10,
∴BC=CN,
∴平行四边形MNCB是菱形,
故,存在t=5秒时,四边形MNCB为菱形.


科目:初中数学 来源: 题型:
【题目】计算:
(1)(+3.41)(0.59)
(2)(13![]() )(13
)(13![]() )
)
(3)20+(14)(18)13
(4)(+3)(21)+(19)+(+12)+(+5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A、B分别表示数a、b,分别计算下列情况中点A、B之间的距离:
(1)当a=2,b=5时,AB=______;
(2)当a=0,b=5时,AB=_____;
(3)当a=2,b=﹣5时,AB=______;
(4)当a=﹣2,b=﹣5时,AB=______;
(5)当a=2,b=m时,AB=______;
(6)数轴上分别表示a和﹣2的两点A和B之间的距离为3,a=____;
(7)点A、B分别表示数a、b,点A、B之间的距离为______;
(8)|a﹣3|+|a﹣2|的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
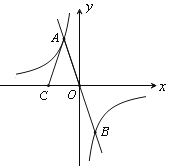
【题目】如图,正比例函数y1=-3x的图象与反比例函数y2=![]() 的图象交于A、B两点,点C在x轴负半轴上,AC=AO,S△ACO=12.
的图象交于A、B两点,点C在x轴负半轴上,AC=AO,S△ACO=12.
(1)求k的值;
(2)当y1>y2时,写出x的取值范围;
(3)当x为何值时,y2<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个质点在第一象限及![]() 轴、
轴、![]() 轴上运动, 在第一秒钟,它从原点运动到
轴上运动, 在第一秒钟,它从原点运动到![]() ,然后接着按图中箭头所示方向运动,且每秒移动一个单位,那么第
,然后接着按图中箭头所示方向运动,且每秒移动一个单位,那么第![]() 秒时质点所在位置的坐标是( )
秒时质点所在位置的坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=![]() ,BE=2.
,BE=2.

求证:(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 ①如图(1),直线l上有2个点,则图中有2条可用图中字母表示的射线,有1条线段
 ;
;
②如图(2),直线l上有3个点,则图中有 条可用图中字母表示的射线,有 条线段;
③如图(3),直线l上有n个点,则图中有 条可用图中字母表示的射线,有 条线段;
④应用(3)中发现的规律解决问题:某校七年级共有8个班进行足球比赛,准备进行循环赛(即每两队之间赛一场),预计全部赛完共需 场比赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.
(1)画出学生测量的示意图;
(2)请你根据以上数据,帮助该同学计算出长江的宽度(精确到0.1 m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
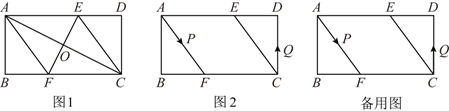
(1)如图1,连接AF、CE求证:四边形AFCE为菱形;
(2)如图1,求AF的长;
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com