
【题目】如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=![]() ,BE=2.
,BE=2.

求证:(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
【答案】证明:(1)连接OC,
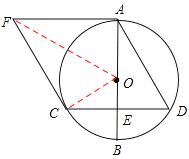
∵AF是⊙O切线,∴AF⊥AB。
∵CD⊥AB,∴AF∥CD。
∵CF∥AD,∴四边形FADC是平行四边形。
∵AB是⊙O的直径,CD⊥AB,
∴![]() 。
。
设OC=x,
∵BE=2,∴OE=x﹣2。
在Rt△OCE中,OC2=OE2+CE2,
∴![]() ,解得:x=4。
,解得:x=4。
∴OA=OC=4,OE=2。∴AE=6。
在Rt△AED中,![]() ,∴AD=CD。
,∴AD=CD。
∴平行四边形FADC是菱形。
(2)连接OF,
∵四边形FADC是菱形,∴FA=FC。
在△AFO和△CFO中,∵ ,∴△AFO≌△CFO(SSS)。
,∴△AFO≌△CFO(SSS)。
∴∠FCO=∠FAO=90°,即OC⊥FC。
∵点C在⊙O上,∴FC是⊙O的切线。
【解析】
试题分析:(1)连接OC,由垂径定理,可求得CE的长,又由勾股定理,可求得半径OC的长,然后由勾股定理求得AD的长,即可得AD=CD,易证得四边形FADC是平行四边形,继而证得四边形FADC是菱形;
(2)连接OF,易证得△AFO≌△CFO,继而可证得FC是⊙O的切线。


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
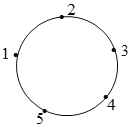
【题目】圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2020次“移位”后,他到达编号为______的点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,AB![]() OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.
OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.
(1)在t=3时,M点坐标 ,N点坐标 ;
(2)当t为何值时,四边形OAMN是矩形?
(3)运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,则tanα的值等于____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的角平分线CF于点F,求证:AE=EF.

经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在疫情期间用![]() 元购进
元购进![]() 两种口罩
两种口罩![]() 个,购买
个,购买![]() 种口罩与购买
种口罩与购买![]() 种口罩的费用相同,且
种口罩的费用相同,且![]() 种口罩的单价是
种口罩的单价是![]() 种口罩单价的
种口罩单价的![]() 倍.
倍.
![]() 求
求![]() 两种口罩的单价各是多少元?
两种口罩的单价各是多少元?
![]() 若计划用不超过
若计划用不超过![]() 元的资金再次购进
元的资金再次购进![]() 两种口罩共
两种口罩共![]() 个,已知
个,已知![]() 两种口罩的进价不变,求
两种口罩的进价不变,求![]() 种口罩最多能购买多少个?
种口罩最多能购买多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com