
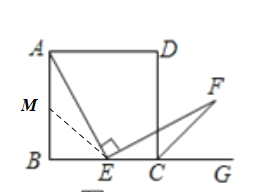
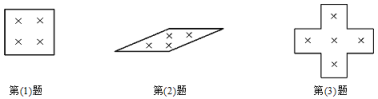
����Ŀ����ѧ���ϣ�����ʦ��ʾ�����⣺��ͼ1���ı���ABCD�������Σ���E�DZ�BC���е㣮��AEF=90������EF�������������DCG�Ľ�ƽ����CF�ڵ�F����֤��AE=EF��

����˼����С��չʾ��һ����ȷ�Ľ���˼·��ȡAB���е�M������ME����AM=EC����֤��AME�ա�ECF������AE=EF��
�ڴ˻����ϣ�ͬѧ�����˽�һ�����о���
��1��Сӱ�������ͼ2�����������E�DZ�BC���е�����Ϊ����E�DZ�BC�ϣ���B��C�⣩������һ�����������������䣬��ô������AE=EF����Ȼ����������ΪСӱ�Ĺ۵���ȷ�������ȷ��д��֤�����̣��������ȷ����˵�����ɣ�
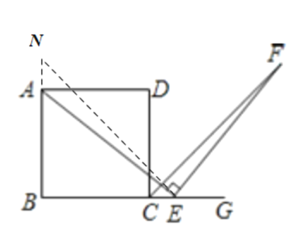
��2��С���������ͼ3����E��BC���ӳ����ϣ���C���⣩������һ�㣬�����������䣬������AE=EF����Ȼ����������ΪС���Ĺ۵���ȷ�������ȷ��д��֤�����̣��������ȷ����˵�����ɣ�
���𰸡���1����ȷ��֤������������2����ȷ��֤��������.
��������
��1����![]() ��ȡһ��
��ȡһ��![]() ��ʹ
��ʹ![]() ������
������![]() ��������֪��������
��������֪��������![]() �ж�
�ж�![]() ����Ϊȫ�������εĶ�Ӧ����ȣ�����
����Ϊȫ�������εĶ�Ӧ����ȣ�����![]() ��
��
��2����![]() ���ӳ�����ȡһ��
���ӳ�����ȡһ��![]() ��ʹ
��ʹ![]() ������
������![]() ��������֪����
��������֪����![]() �ж�
�ж�![]() ����Ϊȫ�������εĶ�Ӧ����ȣ�����
����Ϊȫ�������εĶ�Ӧ����ȣ�����![]() ��
��
�⣺��1����ȷ��
֤������![]() ��ȡһ��
��ȡһ��![]() ��ʹ
��ʹ![]() ������
������![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() �����ƽ���ߣ�
�����ƽ���ߣ�
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��2����ȷ��
֤������ͼʾ����![]() ���ӳ�����ȡһ��
���ӳ�����ȡһ��![]() ��ʹ
��ʹ![]() ������
������![]() ��
��
![]() ��
��
![]() ��
��
![]() ƽ��
ƽ��![]() ��
��
![]() ��
��
![]() ��
��
![]() �ı���
�ı���![]() �������Σ�
��������
![]() ��
��
![]() ��
��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��Ҫʹ�ı���ABCD�������Σ���������һ�����������������������������AB��AD����AC��BD����AB��AD����AC��BD����AB��AD����AB��AD����AB��BD����AB��BD����OB��OC����OB��OC��������ȷ����_____����д��ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����AF����O���ߣ�CD�Ǵ�ֱ��AB���ң�����ΪE������C��DA��ƽ������AF�ཻ�ڵ�F��CD=![]() ��BE=2��
��BE=2��

��֤����1���ı���FADC�����Σ�
��2��FC����O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
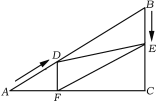
����Ŀ����ͼ����Rt��ABC�У���C=90����AB=60cm����A=30������D�ӵ�A������AB������2cm/����ٶ����B�����˶���ͬʱ��E�ӵ�B������BC������1cm/����ٶ����C�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루0��t��30��������D��DF��AC�ڵ�F������DE��EF��
��1����գ��ı���BEFD��_________��
��2����t=______ʱ���ı���BEFD�ܹ���Ϊ���Ρ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ����ϣ���ʦ����ѧ��ȥ�ⳤ���Ŀ��ȣ�ijѧ���ڳ���������A���۲������ˮ����һ��C�����C��A���Ϸ����ϣ��س�������ǰ��200����B�������C��B��ƫ��30���ķ����ϣ�
��1������ѧ��������ʾ��ͼ��
��2����������������ݣ�������ͬѧ����������Ŀ��ȣ���ȷ��0.1 m����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
Ϊ�ⷽ�̣�x2��1��2��5��x2��1��+4=0�����ǿ��Խ�x2��1��Ϊһ�����壬Ȼ����x2��1=y����ԭ���̻�Ϊy2��5y+4=0����˷��̵ã�y1=1��y2=4��
��y=1ʱ��x2��1�T1����x=��![]() ��
��
��y=4ʱ��x2��1�T4����x=��![]() ��
��
��ԭ���̵Ľ�Ϊ��x1=![]() ��x2=��
��x2=��![]() ��x3=
��x3=![]() ��x4=��
��x4=��![]() ��
��
���Ϸ���������Ԫ���ⷽ�̣��ﵽ�˽��ε�Ŀ�ģ�������ת��˼�룮
�������������ⷽ�̣�x4��8x2+12=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
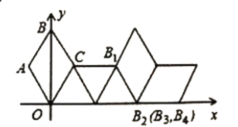
����Ŀ����ͼ��������ϵ�з���һ����OABC����֪��ABC=60�㣬��B��y���ϣ�OA=1���Ƚ�����OABC��x��������������ת��ÿ��ת60�㣬������ת2019�Σ���B���������Ϊ![]() ����
����![]() �������� ��
�������� ��
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ѧ
�� | һ | �� | �� | �� | �� | �� |
1 | 2 | 3 | 4 | 5 | 6 | |
7 | 8 | 9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 |
��1��ķͬѧ��ij�µ�������Ȧ��2��2�����������εķ����ڵ��ĸ����ĺ���48����ô���ĸ�����_______.
��2����Ҳ�������������Ȧ��2��2������б���ڵ��ĸ����ĺ���46�������Ƿֱ���_____.
��3����Ҳ��������Ȧ��5��������ʮ�ֿ��Σ����ǵĺ���55�����м������______.
��4��ij����5�������յĺ���75��������������һ����������______�ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����⣩
��A��B��CΪ���������㣬�����C��A��B֮���ҵ�A�ľ����ǵ�C��B�ľ���3������ô���ǾͳƵ�C��{A��B}����㣮
���磬��ͼ1����A��ʾ����Ϊ��3����B��ʾ����Ϊ1����ʾ0�ĵ�C����A�ľ�����3������B�ľ�����1����ô��C��{A��B}����㣻���磬��ʾ��2�ĵ�D����A�ľ�����1������B�ľ�����3����ô��D�Ͳ���{A��B}����㣬����D��{B��A}����㣮
��֪ʶ���ã�
��ͼ2��M��NΪ���������㣬��M����ʾ����Ϊ��3����N����ʾ����Ϊ5��
��1������������ ����ʾ�ĵ���{M��N}����㣻���������� ����ʾ�ĵ���{N��M}����㣻
��2����ͼ3��A��BΪ���������㣬��A����ʾ����Ϊ��50����B����ʾ����Ϊ30������һ����P�ӵ�B���������˶�����P���˶��������ϵ�ʲôλ��ʱ��P��A��B��ǡ��һ����Ϊ�����������㣿

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com