
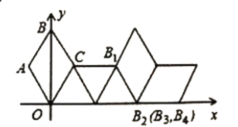
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴正方向无滑动翻转,每次转60°,连续翻转2019次,点B的落点依次为![]() ,则
,则![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,则tanα的值等于____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的角平分线CF于点F,求证:AE=EF.

经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
![]()
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入它所属的集合内:将下列各数填入相应的括号内:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ….
….
正数集合:{ …};
负数集合:{ …};
有理数集合:{ …};
无理数数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在疫情期间用![]() 元购进
元购进![]() 两种口罩
两种口罩![]() 个,购买
个,购买![]() 种口罩与购买
种口罩与购买![]() 种口罩的费用相同,且
种口罩的费用相同,且![]() 种口罩的单价是
种口罩的单价是![]() 种口罩单价的
种口罩单价的![]() 倍.
倍.
![]() 求
求![]() 两种口罩的单价各是多少元?
两种口罩的单价各是多少元?
![]() 若计划用不超过
若计划用不超过![]() 元的资金再次购进
元的资金再次购进![]() 两种口罩共
两种口罩共![]() 个,已知
个,已知![]() 两种口罩的进价不变,求
两种口罩的进价不变,求![]() 种口罩最多能购买多少个?
种口罩最多能购买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为_________cm.

(第16题图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com