
【题目】在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.
(1)画出学生测量的示意图;
(2)请你根据以上数据,帮助该同学计算出长江的宽度(精确到0.1 m).

科目:初中数学 来源: 题型:
【题目】某电脑工程师张先生准备开一家小型电脑公司,欲租一处临街房屋.现有甲、乙两家出租屋,甲家已经装修好,每月租金为3000元;乙家未装修,每月租金为2000元,但若装修成与甲家房屋同样的规格,则需要花装修费4万元.设租用时间为![]() 个月,所需租金为
个月,所需租金为![]() 元.
元.
(1)请分别写出租用甲、乙两家房屋的租金![]() 与租用时间
与租用时间![]() 之间的函数关系;
之间的函数关系;
(2)试判断租用哪家房屋更合算,请写出详细分析过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,AB![]() OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.
OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.
(1)在t=3时,M点坐标 ,N点坐标 ;
(2)当t为何值时,四边形OAMN是矩形?
(3)运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,则tanα的值等于____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a–b|,线段AB的中点表示的数为![]() .
.
(问题情境)如图,数轴上点A表示的数为–2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.
设运动时间为t秒(t>0).
(综合运用)(1)填空:①A、B两点间的距离AB=__________,线段AB的中点表示的数为__________;
②用含t的代数式表示:t秒后,点P表示的数为__________;点Q表示的数为__________.
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的角平分线CF于点F,求证:AE=EF.

经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入它所属的集合内:将下列各数填入相应的括号内:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ….
….
正数集合:{ …};
负数集合:{ …};
有理数集合:{ …};
无理数数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B,C为数轴上的三点,如果点C在点A,B之间,且到点A的距离是点C到点B的距离的3倍,那么我们就称点C是{A,B}的奇妙点.例如,如图①,点A表示的数为-3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇妙点;又如,表示-2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇妙点.
(知识运用)
如图②,M,N为数轴上的两点,点M所表示的数为-2,点N所表示的数为6.
(1)表示数_____的点是{M,N}的奇妙点;表示数______的点是{N,M}的奇妙点;
(2)若点P所表示的数为3,点P是{M,N}的奇妙点,则点M、N所表示的数可以是几?M=______,N=_____(写出一组即可)
(3)如图③,A,B为数轴上的两点,点A所表示的数为-10,点B所表示的数为50.现有一动点P从点A出发向右运动,点P运动到数轴上的什么位置时,P,A,B中恰有一个点为其余两点的奇妙点?

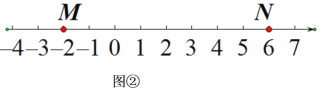
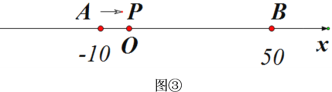
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com