
【题目】某电脑工程师张先生准备开一家小型电脑公司,欲租一处临街房屋.现有甲、乙两家出租屋,甲家已经装修好,每月租金为3000元;乙家未装修,每月租金为2000元,但若装修成与甲家房屋同样的规格,则需要花装修费4万元.设租用时间为![]() 个月,所需租金为
个月,所需租金为![]() 元.
元.
(1)请分别写出租用甲、乙两家房屋的租金![]() 与租用时间
与租用时间![]() 之间的函数关系;
之间的函数关系;
(2)试判断租用哪家房屋更合算,请写出详细分析过程.
【答案】(1)租用甲家房屋时:y=3000x;租用乙家房屋时:y=2000x+40000;(2)①当租用40个月时,两家租金相同;②当租用时间超过40个月时,租乙家的房屋更合算;③当租用时间少于40个月时,租甲家的房屋更合算.
【解析】
(1)根据题目的关系,即可求出关系式;
(2)令甲、乙两家租金相等时,求出月数,然后再进行分析即可.
解:(1)根据题意,
租用甲家房屋时:y=3000x;
租用乙家房屋时:y=2000x+40000;
(2)①由题意,可知:
3000x=2000x+40000,
解得: x=40,
即当租用40个月时,两家租金相同.
②由3000x>2000x+40000,
解得: x>40;
即当租用时间超过40个月时,租乙家的房屋更合算.
③由3000x<2000x+40000,
解得: x<40
即当租用时间少于40个月时,租甲家的房屋更合算.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)(+3.41)(0.59)
(2)(13![]() )(13
)(13![]() )
)
(3)20+(14)(18)13
(4)(+3)(21)+(19)+(+12)+(+5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某核桃种植基地计划种植A、B两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.
(1)若该基地收获两种核桃的年总产量为25800千克,则A、B两种核桃各种植了多少亩?
(2)设该基地种植A种核桃a亩,全部收购后,总收入为w元,求出w与a之间的函数关系式.若要求种植A种核桃的面积不少于B种核桃的一半,那么种植A、B两种核桃各多少亩时,该种植基地的总收入最多?最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC与BD相交于点O.要使四边形ABCD是正方形,还需添加一组条件.下面给出了五组条件:①AB=AD,且AC=BD;②AB⊥AD,且AC⊥BD;③AB⊥AD,且AB=AD;④AB=BD,且AB⊥BD;⑤OB=OC,且OB⊥OC.其中正确的是_____(填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A、B分别表示数a、b,分别计算下列情况中点A、B之间的距离:
(1)当a=2,b=5时,AB=______;
(2)当a=0,b=5时,AB=_____;
(3)当a=2,b=﹣5时,AB=______;
(4)当a=﹣2,b=﹣5时,AB=______;
(5)当a=2,b=m时,AB=______;
(6)数轴上分别表示a和﹣2的两点A和B之间的距离为3,a=____;
(7)点A、B分别表示数a、b,点A、B之间的距离为______;
(8)|a﹣3|+|a﹣2|的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
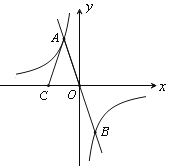
【题目】如图,正比例函数y1=-3x的图象与反比例函数y2=![]() 的图象交于A、B两点,点C在x轴负半轴上,AC=AO,S△ACO=12.
的图象交于A、B两点,点C在x轴负半轴上,AC=AO,S△ACO=12.
(1)求k的值;
(2)当y1>y2时,写出x的取值范围;
(3)当x为何值时,y2<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.
(1)画出学生测量的示意图;
(2)请你根据以上数据,帮助该同学计算出长江的宽度(精确到0.1 m).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com