
【题目】计算:
(1)(+3.41)(0.59)
(2)(13![]() )(13
)(13![]() )
)
(3)20+(14)(18)13
(4)(+3)(21)+(19)+(+12)+(+5)
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这条边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”.已知 RtABC 中,![]() ,一条直角边为1,如果RtABC 是“有趣三角形”,那么这个三角形“有趣中线”的长等于_____
,一条直角边为1,如果RtABC 是“有趣三角形”,那么这个三角形“有趣中线”的长等于_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y-x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
(1)①点A(1,3) 的“坐标差”为 。
②抛物线y=-x2+3x+3的“特征值”为 。
(2)某二次函数y=-x2+bx+c(c≠0) 的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等。
①直接写出m= (用含c的式子表示)
②求此二次函数的表达式。
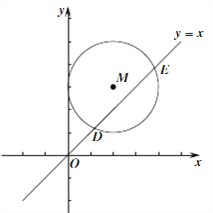
(3)如图,在平面直角坐标系xOy中,以M(2,3)为圆心,2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求若干个相同的不为零的有理数的除法运算叫做除方. 如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把![]() (a≠0)记作a,记作“a 的圈c次方”.
(a≠0)记作a,记作“a 的圈c次方”.
(1)直接写出计算结果:2③= ,(-3)④ = ,![]() ⑤= .
⑤= .
(2)计算 24÷23 + (-8)×2③.
查看答案和解析>>
科目:初中数学 来源: 题型:
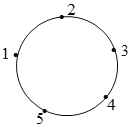
【题目】圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2020次“移位”后,他到达编号为______的点.
查看答案和解析>>
科目:初中数学 来源: 题型:
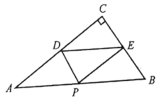
【题目】如图所示,在Rt△ABC中,∠C=90°,BC=6,AC=8, P是斜边AB上一动点,PD⊥AC于点D,PE⊥BC于点E,则DE的长不可能是( )
A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑工程师张先生准备开一家小型电脑公司,欲租一处临街房屋.现有甲、乙两家出租屋,甲家已经装修好,每月租金为3000元;乙家未装修,每月租金为2000元,但若装修成与甲家房屋同样的规格,则需要花装修费4万元.设租用时间为![]() 个月,所需租金为
个月,所需租金为![]() 元.
元.
(1)请分别写出租用甲、乙两家房屋的租金![]() 与租用时间
与租用时间![]() 之间的函数关系;
之间的函数关系;
(2)试判断租用哪家房屋更合算,请写出详细分析过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,AB![]() OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.
OC,点B,C的坐标分别为(15,8),(21,0),动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M,N同时出发,设运动时间为t秒.
(1)在t=3时,M点坐标 ,N点坐标 ;
(2)当t为何值时,四边形OAMN是矩形?
(3)运动过程中,四边形MNCB能否为菱形?若能,求出t的值;若不能,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com