
����Ŀ�����壺��ƽ��ֱ������ϵ�У�ͼ��G�ϵ�P(x,y)��������y���������x�IJ�y��x��ΪP��ġ���������ͼ��G�����е�ġ������е����ֵ��Ϊͼ��G�ġ�����ֵ��
(1)�ٵ�A(1,3) �ġ�����Ϊ ��
��������y=��x2+3x+3�ġ�����ֵ��Ϊ ��
(2)ij���κ���y=��x2+bx+c(c��0) �ġ�����ֵ��Ϊ1����B(m,0)���C�ֱ��Ǵ˶��κ�����ͼ����x���y��Ľ��㣬�ҵ�B���C�ġ�������ȡ�
��ֱ��д��m= (�ú�c��ʽ�ӱ�ʾ)
����˶��κ����ı���ʽ��
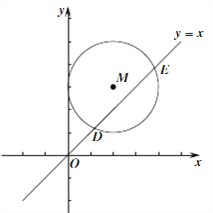
(3)��ͼ����ƽ��ֱ������ϵxOy�У���M(2,3)ΪԲ�ģ�2Ϊ�뾶��Բ��ֱ��y=x�ཻ�ڵ�D��E��ֱ��д����M�ġ�����ֵ��Ϊ ��
���𰸡���1���� 2�� �� 4�� ��2���� m= ��c ; ��
![]() ����3��
����3��![]()
�����������������
��1���������������������Ķ��弴�ɵõ���A��1��3��������
���������Ķ���ɵ������κ���y=��x2+3x+3ͼ���ϵ�������Ϊ�� ![]() �����˹�ϵʽ�䷽�������y-x�����ֵ���Ӷ��õ�������y=��x2+3x+3�ġ�����ֵ����
�����˹�ϵʽ�䷽�������y-x�����ֵ���Ӷ��õ�������y=��x2+3x+3�ġ�����ֵ����
��2����������ɵ���0-m=c-0���ɴ˿ɵ���m=-c��
����m=-c�ɵõ�B������Ϊ��-c��0�����ѵ�B���������![]() �пɵ�
�пɵ�![]() ����
����![]() �ɵ�
�ɵ�![]() ����
����![]() ������
������![]() ������ֵΪ1�ɵã�
������ֵΪ1�ɵã� ![]() �������ɽ��b��c��ֵ���ɴ˼��ɵõ����κ����Ľ���ʽ��
�������ɽ��b��c��ֵ���ɴ˼��ɵõ����κ����Ľ���ʽ��
��3����ͼ������M��ֱ��PF��DE������M�ڵ�P��F������֪������ֱ��PF�Ľ���ʽΪy=-x+5����ֱ��y=x�ϵ����е�������Ϊ0��������ƽ������ֱ��y=x���Ҳ����ֱ��y=xԽԶ�ĵ�������Խ���֪����M�Ͼ���ֱ��y=x��Զ�ĵ��ǵ�P�����P������Ϊ��x��y���ɵ�P��M�ľ���Ϊ2���ɵõ�����x��y�ķ��̣���y=-x+5��ϼ��ɽ�õ�P�����꣬�����Ϳɵõ���M������ֵ��.
���������
��1���� ����A��������1��3����
����A���������3-1= 2��
�� �߶��κ����Ľ���ʽΪ��y=��x2+3x+3��
���ö��κ���ͼ�������е������������ ![]() ��
��
��![]() �����ö��κ���ͼ���ϵ�����������ֵΪ4��
�����ö��κ���ͼ���ϵ�����������ֵΪ4��
��ö��κ���ͼ�������ֵΪ��4��
��2���� ����֪�õ�C������Ϊ��0��c������B������Ϊ��m��0����
���C���������c-0����B���������0-m��
�֡ߵ�B���C�ġ�������ȣ�
��c-0=0-m��
��m=��c��
�� ��m=��c��
��B����c��0����
�������![]() ��
�У�
�ã� ![]() ��
��
��c��0��
��![]() ��
��
��![]() �� ��
�� ��
��![]() �ġ�����Ϊ��
�ġ�����Ϊ��
![]() ��
��
�ߡ�����ֵ��Ϊ1��
��![]() ����
����
���ٴ�����У��ã� ![]()
��![]() ��
��
�������ߵı���ʽΪ![]() ��
��
��3����ͼ������M��ֱ��PF��DE������M�ڵ�P��F��
��ֱ��DE�Ľ���ʽΪ��y=x����M������Ϊ��2��3����
��ֱ��PF�Ľ���ʽΪy=-x+5��
��ֱ��y=x�����е����������0������ֱ��y=x���Ҳ����ֱ��y=xԽԶ�ĵ��������Խ��������M�ϵ�P����ֱ��y=x��Զ��
����P������������M�ġ�����ֵ����
���P��������x��y����
����P����M��2��3���ľ���Ϊ2��
����![]() ��
��
������P��x��y����ֱ��y=-x+5����
��![]() �������
������� ![]() ��
��
����Ӧ���� ![]() ��
��
����P������Ϊ![]() ��
��
����P��������� ![]() ��
��
���M�ġ�����ֵ��Ϊ�� ![]() .
.


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ�����¿�ѧ��ijѧУ������ԭ�е���ˮϵͳ���и��죬�����������5���ʣ�µĹ��������鵥���е�������7.5������깤��Ϊ��������ɹ��̣������������ʩ����6����������������鵥����ɴ���̸���Ҫ�����죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳�ij����Ʒ����Ϊ 70 Ԫ�����ۼ۶�Ϊÿ�� 100 Ԫʱ��ƽ��ÿ������� 20 ��.�����鷢�֣�ÿ����Ʒÿ���� 1 Ԫ���̳�ƽ��ÿ��ɶ��۳� 2 ��.���̳��涨ÿ����Ʒ�������ʲ����� 30%����ÿ����Ʒ���� x Ԫ.
(1)�̳������������� ����ÿ����Ʒӯ�� Ԫ(�ú� x �Ĵ���ʽ��ʾ);
(2)�������������䡢������������£�ÿ����Ʒ���۶���Ԫʱ����ӯ���ɴﵽ 750 Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD��BC��ֱ�ཻ�ڵ�O��AB��CD����BC = 8��AD = 6����AB��CD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90����AD�ǡ�BAC�Ľ�ƽ���ߡ�
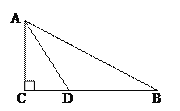
(1)��AB��һ��OΪԲ�ģ�ADΪ������O;
(2)��֤��BCΪ��O�����ߣ�
(3)���AC=3,tanB=![]() ,���O�İ뾶��
,���O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ڹ�·����ʻ�������ߵ�·�̺����õ�ʱ����� �±���ʾ��
ʱ��/t��min�� | 1 | 2.5 | 5 | 10 | 20 | 50 | �� |
·��/s ��km�� | 2 | 5 | 10 | 20 | 40 | 100 | �� |
��1��������仯�����У��Ա��������������ʲô��
��2����������ʻ·��sΪ20kmʱ��������ʱ��t�Ƕ��ٷ��ӣ�
��3���ӱ���˵������t���s�ı仯������ʲô��
��4�����������ʻ��ʱ��Ϊt (min),��ʻ��·��Ϊs ,��ô·��s ��ʱ��t֮��Ĺ�ϵʽΪ .
��5��������һ��ʻ���ɣ���������ʱ��t��300minʱ��������ʻ��·�� s�Ƕ���ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
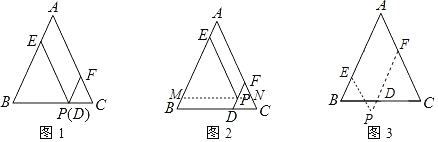
����Ŀ���ڡ�ABC�У�AB��AC����PΪ��ABC����ƽ����һ�����P�ֱ���PE��AC��AB�ڵ�E��PF��AB��BC�ڵ�D����AC�ڵ�F��
��1���۲����
��ͼ1������P��BC����ʱ����ʱ��P��D�غϣ��Բ���PD��PE��PF��AB��������ϵ���� ����
��2�����̽��
��ͼ2������P�ڡ�ABC��ʱ������P��MN��BC��AB�ڵ�M����AC�ڵ�N����д��PD��PE��PF��AB��������ϵ��������֤����
��3���������
��ͼ3������P�ڡ�ABC��ʱ����AB��6��PD��1����ֱ��д��ƽ���ı���PEAF���ܳ��� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1)(+3.41)(0.59)
(2)(13![]() )(13
)(13![]() )
)
(3)20+(14)(18)13
(4)(+3)(21)+(19)+(+12)+(+5)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���A��B�ֱ��ʾ��a��b���ֱ������������е�A��B֮��ľ��룺
��1����a=2��b=5ʱ��AB=______��
��2����a=0��b=5ʱ��AB=_____��
��3����a=2��b=��5ʱ��AB=______��
��4����a=��2��b=��5ʱ��AB=______��
��5����a=2��b=mʱ��AB=______��
��6�������Ϸֱ��ʾa�ͩ�2������A��B֮��ľ���Ϊ3��a=____��
��7����A��B�ֱ��ʾ��a��b����A��B֮��ľ���Ϊ______��
��8��|a��3|+|a��2|����Сֵ��______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com