
【题目】如图,在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线。
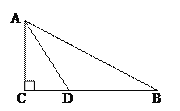
(1)以AB上一点O为圆心,AD为弦作⊙O;
(2)求证:BC为⊙O的切线;
(3)如果AC=3,tanB=![]() ,求⊙O的半径。
,求⊙O的半径。
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:
(1)由题意可知,作线段AD的垂直平分线与AB相交,交点即为圆心O,然后以O为圆心OA为半径作圆即可;
(2)连接OD,由已知易证∠ODA=∠OAD=∠CAD,从而可得OD∥AC,由此可得∠ODB=∠C=90°,结合OD是⊙O的半径即可得到BC和⊙O相切;
(3)由已知条件易得BC=4和AB=5的长度,设⊙O的半径为r,则OD=OA=r,OB=5-r;由OD∥AC可得△BDO∽△BCA,这样由相似三角形对应边成比例即可列出关于r的方程,解方程即可求得r的值.
试题解析:
(1)如图所示,⊙O为所求圆;
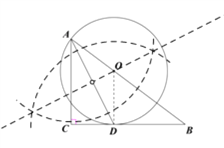
(2)连接OD.
∵AD平分∠CAB
∴∠CAD=∠BAD
又∵OA=OD
∴∠OAD=∠ODA
∴∠CAD=∠ODA
∴OD∥AC
∴∠ODB=∠C=90°
又∵OD为半径
∴BC是⊙O的切线.
(3)∵在△ABC中,AC=3,tanB=![]() ,∠C=90°,
,∠C=90°,
∴BC=4,AB=5,
设⊙O的半径为r,则OA=OD=r,BO=5-r
∵OD∥AC
∴△BOD∽△BAC
∴![]()
即 ![]()
解得, ![]() ,
,
∴⊙O的半径为 ![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.

(1)圆心O到CD的距离是______;
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】脱式计算(能简算的要简算,并写出简算过程)
①6.8×101-68×0.1
②2.5×(2.9+2.9+5.8)
③5.8÷(![]() )
)
④![]()
⑤3.25×![]() -3.25×
-3.25×![]() +2×325%
+2×325%
⑥![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中点A的坐标为(0,6),点B的坐标为(﹣![]() ,5),将△AOB沿x轴向左平移得到△A′O′B′,点A的对应点A′落在直线y=﹣
,5),将△AOB沿x轴向左平移得到△A′O′B′,点A的对应点A′落在直线y=﹣![]() x上,则点B的对应点B′的坐标为( )
x上,则点B的对应点B′的坐标为( )
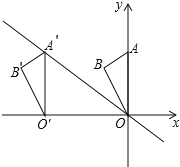
A.(﹣8,6)B.(﹣![]() ,5)C.(﹣
,5)C.(﹣![]() ,5)D.(﹣8,5)
,5)D.(﹣8,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y-x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
(1)①点A(1,3) 的“坐标差”为 。
②抛物线y=-x2+3x+3的“特征值”为 。
(2)某二次函数y=-x2+bx+c(c≠0) 的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等。
①直接写出m= (用含c的式子表示)
②求此二次函数的表达式。
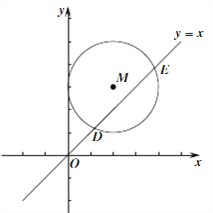
(3)如图,在平面直角坐标系xOy中,以M(2,3)为圆心,2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的最小正整数),并且运算重复进行.例如:取n=26,则运算过程如图:
为奇数的最小正整数),并且运算重复进行.例如:取n=26,则运算过程如图:
![]()
那么当n=26时,第2016次“F运算”的结果是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求若干个相同的不为零的有理数的除法运算叫做除方. 如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把![]() (a≠0)记作a,记作“a 的圈c次方”.
(a≠0)记作a,记作“a 的圈c次方”.
(1)直接写出计算结果:2③= ,(-3)④ = ,![]() ⑤= .
⑤= .
(2)计算 24÷23 + (-8)×2③.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com