
����Ŀ��һ�������ڹ�·����ʻ�������ߵ�·�̺����õ�ʱ����� �±���ʾ��
ʱ��/t��min�� | 1 | 2.5 | 5 | 10 | 20 | 50 | �� |
·��/s ��km�� | 2 | 5 | 10 | 20 | 40 | 100 | �� |
��1��������仯�����У��Ա��������������ʲô��
��2����������ʻ·��sΪ20kmʱ��������ʱ��t�Ƕ��ٷ��ӣ�
��3���ӱ���˵������t���s�ı仯������ʲô��
��4�����������ʻ��ʱ��Ϊt (min),��ʻ��·��Ϊs ,��ô·��s ��ʱ��t֮��Ĺ�ϵʽΪ .
��5��������һ��ʻ���ɣ���������ʱ��t��300minʱ��������ʻ��·�� s�Ƕ���ǧ�ף�
���𰸡���1���Ա�����ʱ�䣬�������·�̣���2��10min����3������t���s���4��s=2t����5��60ǧ��
��������
��1�������Ա�����������Ķ���д�����ɣ���2�����ݱ���ֱ��д��������ʻ·��sΪ20kmʱ�伴�ɣ���3�����ݱ���ֱ��д������t���s�ı仯���ƣ���4��ͨ��·��=�ٶȡ�ʱ�䣬д����ϵʽ���ɣ���5��ͨ����4���Ĺ�ϵʽֱ���������.
1���Ա�����ʱ�䣬�������·�̣�
��2���ߵ�t=1ʱ��s=2��
��v=![]() =2km/min��
=2km/min��
t=![]() =10min��
=10min��
���ߴӱ���ֱ�ӹ۲�ó���
��3���ɱ��ã�����t���s�����ʱ��ÿ����1���ӣ�·������2ǧ�ף���
��4���ɣ�2����v=2��
��·��s��ʱ��t֮��Ĺ�ϵʽΪs=2t���ʴ�Ϊs=2t��
��5����t=300����s=2t����s=600km��


 �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ů������5��д�Ų�ͬ���ֵĿ�Ƭ�����㰴Ҫ��ѡ��Ƭ��������и����⣺
![]()
��1������ѡ�����ſ�Ƭ��ʹ�����ſ�Ƭ�����ֵij˻����
�����ſ�Ƭ�ϵ����ֱַ��� ����Ϊ _��
��2������ѡ�����ſ�Ƭ��ʹ�����ſ�Ƭ���������������С��
�����ſ�Ƭ�ϵ����ֱַ��� ����Ϊ ��
��3������ѡ��4�ſ�Ƭ��ÿ�ſ�Ƭ�ϵ�����ֻ����һ�Σ�ѡ��ӡ������ˡ����е��ʵ��������ɼ����ţ���ʹ��������Ϊ24��д������ʽ�ӣ���д��һ�ּ��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB��90����sinA��![]() ��BC��8����D��AB���е㣬����B��CD�Ĵ��ߣ�����Ϊ��E.
��BC��8����D��AB���е㣬����B��CD�Ĵ��ߣ�����Ϊ��E.
(1)���߶�CD�ij���
(2)��cos��ABE��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=x2+bx+c��x�ύ�ڵ�A(��2,0).
(1)��գ�c= (�ú�b��ʽ�ӱ�ʾ)��
(2)��b��4
����֤����������x�����������㣻
������������x�����һ������ΪB�����߶�AB��ǡ��5�����㣨�����ꡢ�����궼�������ĵ㣩��ֱ��д��b��ȡֵ��ΧΪ ��
(3)ֱ��y=x��4����������y=x2+bx+c�Ķ���P���������ߵı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У�ͼ��G�ϵ�P(x,y)��������y���������x�IJ�y��x��ΪP��ġ���������ͼ��G�����е�ġ������е����ֵ��Ϊͼ��G�ġ�����ֵ��
(1)�ٵ�A(1,3) �ġ�����Ϊ ��
��������y=��x2+3x+3�ġ�����ֵ��Ϊ ��
(2)ij���κ���y=��x2+bx+c(c��0) �ġ�����ֵ��Ϊ1����B(m,0)���C�ֱ��Ǵ˶��κ�����ͼ����x���y��Ľ��㣬�ҵ�B���C�ġ�������ȡ�
��ֱ��д��m= (�ú�c��ʽ�ӱ�ʾ)
����˶��κ����ı���ʽ��
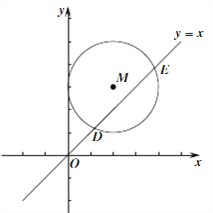
(3)��ͼ����ƽ��ֱ������ϵxOy�У���M(2,3)ΪԲ�ģ�2Ϊ�뾶��Բ��ֱ��y=x�ཻ�ڵ�D��E��ֱ��д����M�ġ�����ֵ��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1������6������+15��+4������15��
��2����2��3������4����2+3
��3����![]() ��
��![]()
![]() ��������24��
��������24��
��4����14��2������3��2������![]() ��
��
��5����18������3��2+5������2��3������15����5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������Ȥ�С����Χ��һ����������������һ�߿�ǽ�����������ɳ�Ϊ30�����Χ�ɣ���֪ǽ��Ϊ18�ף���ͼ��ʾ���������������ֱ��ǽ��һ�߳�Ϊx�ף�
��1�������������Ϊ72ƽ���ף���x��
��2����ƽ����ǽ��һ�߳���С��8�ף������������������ֵ����Сֵ������У�������ֵ����Сֵ�����û�У���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
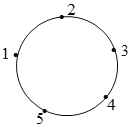
����Ŀ��Բ��������㣬������㽫Բ�ֳ���ȷ�(ÿһ�ݳ�Ϊһ�λ���)����������㰴˳ʱ�뷽�����α��Ϊ1��2��3��4��5������ijһ�㿪ʼ����Բ��˳ʱ�뷽�����ߣ���ı�������ּ��������λ�������������߷�Ϊһ�Ρ���λ�����磺С���ڱ��Ϊ3�ĵ㣬��ô��Ӧ��3�λ���������3�� 4��5��1Ϊ��һ�Ρ���λ������ʱ��������Ϊ1�ĵ㣬Ȼ���1��2Ϊ�ڶ��Ρ���λ������С���ӱ��Ϊ4�ĵ㿪ʼ����2020�Ρ���λ������������Ϊ______�ĵ㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��BC��2����ABΪֱ���ġ�O�ֱ�BC��AC�ڵ�D��E���ҵ�DΪBC���е㣮
��1����֤����ABCΪ�ȱ������Σ�
��2����DE�ij���
��3�����߶�AB���ӳ������Ƿ����һ��P��ʹ��PBD�ա�AED�������ڣ������PB�ij����������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com