
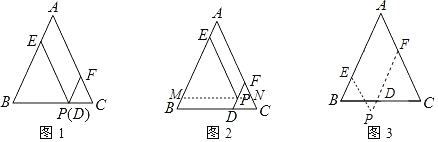
【题目】在△ABC中,AB=AC,点P为△ABC所在平面内一点过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
(1)观察猜想
如图1,当点P在BC边上时,此时点P、D重合,试猜想PD,PE,PF与AB的数量关系: .
(2)类比探究
如图2,当点P在△ABC内时,过点P作MN∥BC交AB于点M,交AC于点N,试写出PD,PE,PF与AB的数量关系,并加以证明.
(3)解决问题
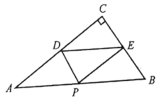
如图3,当点P在△ABC外时,若AB=6,PD=1,请直接写出平行四边形PEAF的周长 .
【答案】(1)PD+PE+PF=AB;(2)PD+PE+PF=AB,见解析;(3)14
【解析】
(1)由PE∥AC,PF∥AB可判断四边形AEPF为平行四边形,根据平行线的性质得∠1=∠C,根据平行四边形的性质得PF=AE,再根据等腰三角形的性质得∠B=∠C,则∠B=∠1,则可根据等腰三角形的判定得PE=BE,所以PE+PF=AB;
(2)因为四边形PEAF为平行四边形,所以PE=AF,又三角形FDC为等腰三角形,所以FD=PF+PD=FC,即PE+PD+PF=AC=AB;
(3)过点P作MN∥BC分别交AB、AC于M、N两点,推出PE+PF=AM,再推出MB=PD即可得到结论.
解:(1)答:PD+PE+PF=AB.
证明如下:∵点P在BC上,
∴PD=0,
∵PE∥AC,PF∥AB,
∴四边形PFAE是平行四边形,
∴PF=AE,
∵PE∥AC,
∴∠BPE=∠C,
∴∠B=∠BPE,
∴PE=BE,
∴PE+PF=BE+AE=AB,
∵PD=0,
∴PD+PE+PF=AB,
故答案为:PD+PE+PF=AB;
(2)如图2,结论成立:PD+PE+PF=AB.

证明:过点P作MN∥BC分别交AB,AC于M,N两点,
∵PE∥AC,PF∥AB,
∴四边形AEPF是平行四边形,
∵MN∥BC,PF∥AB,
∴四边形BDPM是平行四边形,
∴AE=PF,∠EPM=∠ANM=∠C,
∵AB=AC,
∴∠EMP=∠B,
∴∠EMP=∠EPM,
∴PE=EM,
∴PE+PF=AE+EM=AM.
∵四边形BDPM是平行四边形,
∴MB=PD.
∴PD+PE+PF=MB+AM=AB,
即PD+PE+PF=AB;
(3)如图3,过点P作MN∥BC分别交AB、AC延长线于M、N两点.
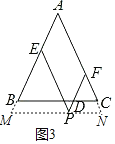
∵PE∥AC,PF∥AB,
∴四边形PEAF是平行四边形,
∴PF=AE,
∵AB=AC,
∴∠B=∠C,
∵MN∥BC,
∴∠ANM=∠C=∠B=∠AMN,
∵PE∥AC,
∴∠EPM=∠FNP,
∴∠AMN=∠FPN,
∴∠EPM=∠EMP,
∴PE=ME,
∵AE+ME=AM,
∴PE+PF=AM,
∵MN∥CB,DF∥AB,
∴四边形BDPM是平行四边形,
∴MB=PD,
∴PE+PF﹣PD=AM﹣MB=AB,
∴PE+PF=AB+PD=6+1=7,
∴平行四边形PEAF的周长=14,
故答案为:14.


科目:初中数学 来源: 题型:
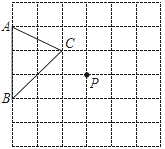
【题目】如图,在正方形网格中,每一小正方形的边长为1,格点△ABC(三个顶点在相应的小正方形的顶点处)在如图所示的位置:
(1) △ABC的面积为___________ 直接写出)
(2) 在网格中画出线段AB绕格点P顺时针旋转90°之后的对应线段A1B1(点A1对应点A)
(3) 在(2)的基础上直接写出![]() =___________
=___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】脱式计算(能简算的要简算,并写出简算过程)
①6.8×101-68×0.1
②2.5×(2.9+2.9+5.8)
③5.8÷(![]() )
)
④![]()
⑤3.25×![]() -3.25×
-3.25×![]() +2×325%
+2×325%
⑥![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y-x称为P点的“坐标差”,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
(1)①点A(1,3) 的“坐标差”为 。
②抛物线y=-x2+3x+3的“特征值”为 。
(2)某二次函数y=-x2+bx+c(c≠0) 的“特征值”为1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等。
①直接写出m= (用含c的式子表示)
②求此二次函数的表达式。
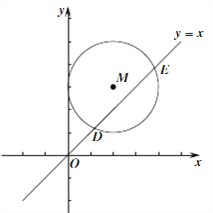
(3)如图,在平面直角坐标系xOy中,以M(2,3)为圆心,2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的最小正整数),并且运算重复进行.例如:取n=26,则运算过程如图:
为奇数的最小正整数),并且运算重复进行.例如:取n=26,则运算过程如图:
![]()
那么当n=26时,第2016次“F运算”的结果是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求若干个相同的不为零的有理数的除法运算叫做除方. 如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把![]() (a≠0)记作a,记作“a 的圈c次方”.
(a≠0)记作a,记作“a 的圈c次方”.
(1)直接写出计算结果:2③= ,(-3)④ = ,![]() ⑤= .
⑤= .
(2)计算 24÷23 + (-8)×2③.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠C=90°,BC=6,AC=8, P是斜边AB上一动点,PD⊥AC于点D,PE⊥BC于点E,则DE的长不可能是( )
A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,则下列说法:
①当0<x<2时, y1>y2;②y1随x的增大而增大的取值范围是x<2;③使得y2大于4的x值不存在;④若y1=2,则x=2﹣![]() 或x=1.其中正确的有( )
或x=1.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com