
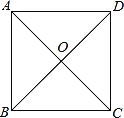
【题目】在平行四边形ABCD中,对角线AC与BD相交于点O.要使四边形ABCD是正方形,还需添加一组条件.下面给出了五组条件:①AB=AD,且AC=BD;②AB⊥AD,且AC⊥BD;③AB⊥AD,且AB=AD;④AB=BD,且AB⊥BD;⑤OB=OC,且OB⊥OC.其中正确的是_____(填写序号).
【答案】①②③⑤
【解析】
】由矩形、菱形、正方形的判定方法对各个选项进行判断即可.
∵四边形ABCD是平行四边形,AB=AD,
∴四边形ABCD是菱形,
又∵AC=BD,
∴四边形ABCD是正方形,①正确;
∵四边形ABCD是平行四边形,AB⊥AD,
∴四边形ABCD是矩形,
又∵AC⊥BD,
∴四边形ABCD是正方形,②正确;
∵四边形ABCD是平行四边形,AB⊥AD,
∴四边形ABCD是矩形,
又∵AB=AD,
∴四边形ABCD是正方形,③正确;
④AB=BD,且AB⊥BD,无法得出四边形ABCD是正方形,故④错误;
∵四边形ABCD是平行四边形,OB=OC,
∴四边形ABCD是矩形,
又∵OB⊥OC,
∴四边形ABCD是正方形,⑤正确;
故答案为:①②③⑤.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c与x轴交于点A(-2,0).
(1)填空:c= (用含b的式子表示)。
(2)若b<4
①求证:抛物线与x轴有两个交点;
②设抛物线与x轴的另一个交点为B,当线段AB上恰有5个整点(横坐标、纵坐标都是整数的点),直接写出b的取值范围为 ;
(3)直线y=x-4经过抛物线y=x2+bx+c的顶点P,求抛物线的表达式。
查看答案和解析>>
科目:初中数学 来源: 题型:
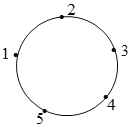
【题目】圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2020次“移位”后,他到达编号为______的点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月25日,中国国际大数据产业博览会在贵阳会展中心开幕,博览会设了编号为1~6号展厅共6个,小雨一家计划利用两天时间参观其中两个展厅:第一天从6个展厅中随机选择一个,第二天从余下的5个展厅中再随机选择一个,且每个展厅被选中的机会均等.
(1)第一天,1号展厅没有被选中的概率是 ;
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑工程师张先生准备开一家小型电脑公司,欲租一处临街房屋.现有甲、乙两家出租屋,甲家已经装修好,每月租金为3000元;乙家未装修,每月租金为2000元,但若装修成与甲家房屋同样的规格,则需要花装修费4万元.设租用时间为![]() 个月,所需租金为
个月,所需租金为![]() 元.
元.
(1)请分别写出租用甲、乙两家房屋的租金![]() 与租用时间
与租用时间![]() 之间的函数关系;
之间的函数关系;
(2)试判断租用哪家房屋更合算,请写出详细分析过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的角平分线CF于点F,求证:AE=EF.

经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com