
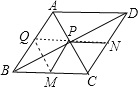
【题目】已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=___.

【答案】5.
【解析】
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
解:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=![]() AC=3,BP=
AC=3,BP=![]() BD=4,
BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故答案为5


科目:初中数学 来源: 题型:
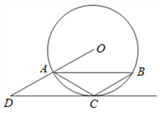
【题目】如图,△ABC内接于⊙O,CA=CB,CD∥AB,CD与OA的延长线交于点D.
(1)求证:CD 是⊙O 的切线;
(2)若∠ACB=120°,OA=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图象法求方程的解,体现了数形结合的方法,它是将方程的解看成两个函数图象交点的横坐标.若关于x的方程x2+a﹣![]() =0(a>0)只有一个整数解,则a的值等于 .
=0(a>0)只有一个整数解,则a的值等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一块长方形花园(如图一所示),长为![]() 米,宽为
米,宽为![]() 米,现准备在花园中间修建横竖两条小路(图中空白部分),已知横向小路的宽是竖向小路的宽的
米,现准备在花园中间修建横竖两条小路(图中空白部分),已知横向小路的宽是竖向小路的宽的![]() 倍,设竖向小路的宽为
倍,设竖向小路的宽为![]() 米(
米(![]() 为正数).
为正数).
(![]() )两条小路的面积之和是多少?
)两条小路的面积之和是多少?
(![]() )当
)当![]() 时,求花园剩余部分(阴影部分)的面积;
时,求花园剩余部分(阴影部分)的面积;
(3)若把竖向小路的宽改为原来的![]() 倍、横向小路的宽改为原来的一半(如图二所示),设图一与图二中花园剩余部分的面积分别为
倍、横向小路的宽改为原来的一半(如图二所示),设图一与图二中花园剩余部分的面积分别为![]() 、
、![]() ,求
,求![]() 与
与![]() 的差.
的差.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为 ;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.
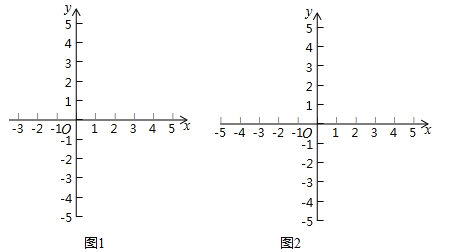
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某司机在东西路上开车接送乘客,他早晨从A地出发,(去向东的方向正方向),到晚上送走最后一位客人为止,他一天行驶的的里程记录如下(单位:㎞)
+10 ,— 5, —15 ,+ 30 ,—20 ,—16 ,+ 14
(1) 若该车每百公里耗油 3 L ,则这车今天共耗油 多少升?
(2) 据记录的情况,你能否知道该车送完最后一个乘客是,他在A地的什么方向?距A地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
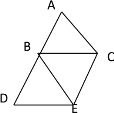
【题目】如图,等边三角形ABC沿边AB方向平移到△BDE的位置,则图中∠CBE=_____,连接CE后,线段CE与AD的关系是______,△BEC为____三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点D,E分别是△ABC的BC,AC边的中点.
(1)如图①,若AB=10,求DE的长;
(2)如图②,点F是AB边上的一点,FG//AD,交ED的延长线于点G.求证:AF=DG

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com