Question

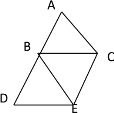
【题目】如图，等边三角形ABC沿边AB方向平移到△BDE的位置，则图中∠CBE=_____，连接CE后，线段CE与AD的关系是______，△BEC为____三角形.

Answer 1

【答案】60° CE∥AD且AD＝2CE 等边

【解析】

由题意易得平移的距离是等边三角形的边长，然后根据经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等来解答即可．

解：∵等边三角形ABC沿边AB方向平移到△BDE的位置，

∴平移的距离等于等边三角形的边长AB，

由平移的性质可知∠BAC=∠DBE=60°，AB＝BD，BE＝AC，CE∥AD，

∴∠CBE=180°－∠ABC－∠DBE＝180°－60°－60°＝60°，

则△CBE是正三角形，

∴CE＝AB，

∴AD＝2CE.

则图中∠CBE＝60°，线段CE与AD的关系是：CE∥AD 且AD＝2CE，△CBE为等边三角形，

故答案为：60°；CE∥AD 且AD＝2CE；等边.