
【题目】在一节数学课上,老师布置了一个任务:如图1,在Rt△ABC中,∠B=90°,用尺规作图作矩形ABCD.同学们开动脑筋,想出了很多办法,其中小亮作图如图2,他向同学们分享了作法:
①分别以点A、C为圆心,大于![]() AC长为半径画弧,两弧分别交于点E、F,连接E、F交AC于点O;
AC长为半径画弧,两弧分别交于点E、F,连接E、F交AC于点O;
②作射线BO,在BO上取点D,使OD=OB;
③连结AD、CD则四边形ABCD就是所求作的矩形.
请用文字写出小亮的每一步作图的依据① ;② ;③ .

【答案】到线段两端距离相等的点在线段的垂直平分线上;直角三角形斜边上的中线等于斜边的一半;对角线互相平分且相等的四边形是矩形
【解析】
根据到线段两端距离相等的点在线段的垂直平分线上可判断EF垂直平分AC,再根据直角三角形斜边上的中线等于斜边的一半得到BO=OA=OC,则由OD=OB得到BO=OA=OC=OD,从而根据矩形的判定方法可判断四边形ABCD就是所求作的矩形.
由作法得EF垂直平分AC,则OA=OC,
则BO为Rt△ABC斜边上的中线,
∴BO=OA=OC,
∵OD=OB,
∴BO=OA=OC=OD,
∴四边形ABCD为矩形.
∴小亮的作图依据为:①到线段两端距离相等的点在线段的垂直平分线上;②直角三角形斜边上的中线等于斜边的一半;③对角线互相平分且相等的四边形是矩形.
故答案为:到线段两端距离相等的点在线段的垂直平分线上,直角三角形斜边上的中线等于斜边的一半,对角线互相平分且相等的四边形是矩形.


科目:初中数学 来源: 题型:
【题目】如图,过点 A(1,0)作x轴的垂线,交反比例函数 y=![]() (x大于零)的图象交于点M,已知三角形AOM的面积为3.
(x大于零)的图象交于点M,已知三角形AOM的面积为3.
(1)求k的值;
(2)设点B的坐标为(t,0), 若以AB为一边的正方形ABCD有顶点在该反比例函数的图像上,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一块长方形花园(如图一所示),长为![]() 米,宽为
米,宽为![]() 米,现准备在花园中间修建横竖两条小路(图中空白部分),已知横向小路的宽是竖向小路的宽的
米,现准备在花园中间修建横竖两条小路(图中空白部分),已知横向小路的宽是竖向小路的宽的![]() 倍,设竖向小路的宽为
倍,设竖向小路的宽为![]() 米(
米(![]() 为正数).
为正数).
(![]() )两条小路的面积之和是多少?
)两条小路的面积之和是多少?
(![]() )当
)当![]() 时,求花园剩余部分(阴影部分)的面积;
时,求花园剩余部分(阴影部分)的面积;
(3)若把竖向小路的宽改为原来的![]() 倍、横向小路的宽改为原来的一半(如图二所示),设图一与图二中花园剩余部分的面积分别为
倍、横向小路的宽改为原来的一半(如图二所示),设图一与图二中花园剩余部分的面积分别为![]() 、
、![]() ,求
,求![]() 与
与![]() 的差.
的差.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某司机在东西路上开车接送乘客,他早晨从A地出发,(去向东的方向正方向),到晚上送走最后一位客人为止,他一天行驶的的里程记录如下(单位:㎞)
+10 ,— 5, —15 ,+ 30 ,—20 ,—16 ,+ 14
(1) 若该车每百公里耗油 3 L ,则这车今天共耗油 多少升?
(2) 据记录的情况,你能否知道该车送完最后一个乘客是,他在A地的什么方向?距A地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与坐标轴分别交于A、B点,AE平分
的图象与坐标轴分别交于A、B点,AE平分![]() ,交
,交![]() 轴于点E.
轴于点E.

(1)直接写出点A和点B的坐标.
(2)求直线AE的表达式.
(3)过点B作BF![]() AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交
AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交![]() 轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
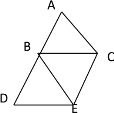
【题目】如图,等边三角形ABC沿边AB方向平移到△BDE的位置,则图中∠CBE=_____,连接CE后,线段CE与AD的关系是______,△BEC为____三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部数学专著,其中有这样一道名题:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几步及之?”意思是说:走路快的人走100步的时候,走路慢的才走了60步,走路慢的人先走100步,然后走路快的人去追赶,问走路快的人要走多少部才能追上?若设走路快的人要走x步才能追上走路慢的人,此时走路慢的人又走了y步,根据题意可列方程组为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知反比例函数![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
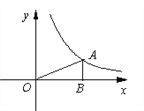
(1)该函数图象的另一分支位于第_____象限,m的取值范围是____________;
(2)已知点A在反比例函数图象上,AB⊥x轴于点B,△AOB的面积为3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解决问题:
求1+2+22+23+…...+22014的值,另S=1+2+22+23+…...+22014,
等式两边同时乘2,得2S=2+22+23+.......+22014+22015
两式相减,得2S - S = 22015 -1 所以S = 22015 - 1
依据以上计算方法,计算:1 + 3 + 32 + ..... + 32019
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com