
【题目】某核桃种植基地计划种植A、B两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.
(1)若该基地收获两种核桃的年总产量为25800千克,则A、B两种核桃各种植了多少亩?
(2)设该基地种植A种核桃a亩,全部收购后,总收入为w元,求出w与a之间的函数关系式.若要求种植A种核桃的面积不少于B种核桃的一半,那么种植A、B两种核桃各多少亩时,该种植基地的总收入最多?最多是多少元?
【答案】(1)A、B两种核桃各种植了21亩和9亩.(2)种植A、B两种核桃各10亩、20亩时,该种植基地的总收入最多,最多是113600元.
【解析】试题分析:(1)设该基地种植A种水果x亩,种植B种水果(30-x)亩,根据总产量的等量关系,可得一元一次方程,解一元一次方程即可解答;
(2)设该基地种植A种水果a亩,种植B种水果(30-a)亩,根据种植面积的关系可得a≥![]() (30-a),求解可得a的取值范围,根据题意得到w和a的关系式,利用一次函数的性质即可解答.
(30-a),求解可得a的取值范围,根据题意得到w和a的关系式,利用一次函数的性质即可解答.
解:(1)设A种核桃种植了x亩,由题意可得800x+1000(30-x)=25800,解得x=21,∴30-x=9.即A、B两种核桃各种植了21亩和9亩.
(2)由题意可得w=800a×4.2+1000(30-a)×4=120000-640a,即w与a之间的函数关系式为w=120000-640a.∵a≥![]() (30-a),∴a≥10,∴当a=10时,w=120000-640a取得最大值,此时w=113600,30-a=20,即种植A、B两种核桃各10亩、20亩时,该种植基地的总收入最多,最多是113600元.
(30-a),∴a≥10,∴当a=10时,w=120000-640a取得最大值,此时w=113600,30-a=20,即种植A、B两种核桃各10亩、20亩时,该种植基地的总收入最多,最多是113600元.


科目:初中数学 来源: 题型:
【题目】脱式计算(能简算的要简算,并写出简算过程)
①6.8×101-68×0.1
②2.5×(2.9+2.9+5.8)
③5.8÷(![]() )
)
④![]()
⑤3.25×![]() -3.25×
-3.25×![]() +2×325%
+2×325%
⑥![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求若干个相同的不为零的有理数的除法运算叫做除方. 如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把![]() (a≠0)记作a,记作“a 的圈c次方”.
(a≠0)记作a,记作“a 的圈c次方”.
(1)直接写出计算结果:2③= ,(-3)④ = ,![]() ⑤= .
⑤= .
(2)计算 24÷23 + (-8)×2③.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠C=90°,BC=6,AC=8, P是斜边AB上一动点,PD⊥AC于点D,PE⊥BC于点E,则DE的长不可能是( )
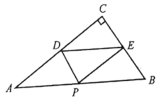
A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑工程师张先生准备开一家小型电脑公司,欲租一处临街房屋.现有甲、乙两家出租屋,甲家已经装修好,每月租金为3000元;乙家未装修,每月租金为2000元,但若装修成与甲家房屋同样的规格,则需要花装修费4万元.设租用时间为![]() 个月,所需租金为
个月,所需租金为![]() 元.
元.
(1)请分别写出租用甲、乙两家房屋的租金![]() 与租用时间
与租用时间![]() 之间的函数关系;
之间的函数关系;
(2)试判断租用哪家房屋更合算,请写出详细分析过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,则下列说法:
①当0<x<2时, y1>y2;②y1随x的增大而增大的取值范围是x<2;③使得y2大于4的x值不存在;④若y1=2,则x=2﹣![]() 或x=1.其中正确的有( )
或x=1.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a–b|,线段AB的中点表示的数为![]() .
.
(问题情境)如图,数轴上点A表示的数为–2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.
设运动时间为t秒(t>0).
(综合运用)(1)填空:①A、B两点间的距离AB=__________,线段AB的中点表示的数为__________;
②用含t的代数式表示:t秒后,点P表示的数为__________;点Q表示的数为__________.
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
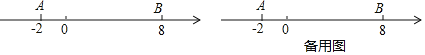
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com