
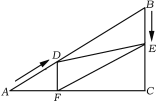
【题目】如图,在Rt△ABC中,∠C=90°,AB=60cm,∠A=30°,点D从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,同时点E从点B出发沿BC方向以1cm/秒的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤30).过点D作DF⊥AC于点F,连接DE,EF.
(1)填空:四边形BEFD是_________;
(2)当t=______时,四边形BEFD能够成为菱形。
(3)当t为何值时?△DEF为直角三角形.
【答案】(1)平行四边形;(2)20;(3)t=15或24秒时,△DEF为直角三角形.
【解析】
(1)利用t表示出BE的长,利用直角三角形的性质求得DF的长,然后根据平行四边形的判定解答即可;
(2)由菱形的性质可得关于t的方程,解方程即得结果;
(3)分三种情况:显然∠DFE<90°;当∠EDF=90°时,如图1,利用矩形的性质和30°角的直角三角形的性质可得关于t的方程,解方程即得结果;当∠DEF=90°时,如图2,易得∠BDE=90°,然后利用30°角的直角三角形的性质解答.
证明:(1)∵∠A=30°,DF⊥AC,AD=2t,BE=t,
∴DF=![]() AD=t=BE,
AD=t=BE,
∵DF⊥AC,BC⊥AC,
∴DF∥BE,且DF=BE,
∴四边形BEFD是平行四边形;
故答案为:平行四边形;
(2)当BD=BE时,四边形BEFD能够成为菱形,
此时60﹣2t=t,∴t=20,
∴当t=20s,四边形BEFD能够成为菱形;
故答案为:20;
(3)∵∠DFE<∠DFC,∴∠DFE<90°;
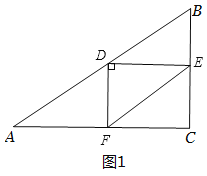
当∠EDF=90°时,如图1,
∵∠ACB=∠EDF=∠CFD=90°,
∴四边形DECF是矩形,
∴DF=EC=t,
∵∠C=90°,AB=60cm,∠A=30°,
∴![]() cm,
cm,
∴t=30﹣t,
∴t=15;
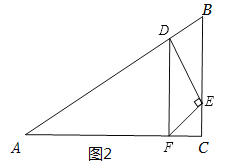
当∠DEF=90°,如图2,
∵四边形BEFD是平行四边形,
∴BD∥EF,
∴∠BDE=∠DEF=90°,且∠B=60°,
∴∠DEB=30°,
∴BE=2BD,
∴2(60﹣2t)=t,
∴t=24.
综上所述:当t=15或24秒时,△DEF为直角三角形.


科目:初中数学 来源: 题型:
【题目】2017年5月25日,中国国际大数据产业博览会在贵阳会展中心开幕,博览会设了编号为1~6号展厅共6个,小雨一家计划利用两天时间参观其中两个展厅:第一天从6个展厅中随机选择一个,第二天从余下的5个展厅中再随机选择一个,且每个展厅被选中的机会均等.
(1)第一天,1号展厅没有被选中的概率是 ;
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,则tanα的值等于____

查看答案和解析>>
科目:初中数学 来源: 题型:
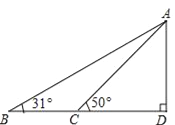
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的角平分线CF于点F,求证:AE=EF.

经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
![]()
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】儿童服装店老板以50元的价格购进20件衣服,针对不同的顾客,20件衣服的售价不完全相同,若以68元为标准,将超出的钱数记为正,不足的钱数记为负,记录结果如下表:
售出件数 | 5 | 4 | 2 | 1 | 7 | 1 |
售价 | +2 | +3 | +1 | 0 | —2 | —1 |
(1)问该服装店售完这20件衣服后,赚了多少钱?
(2)老板为了促销,对购买价格不低于标准的每个顾客送了价值5元的小礼物,如果不考虑其他因素,这20件衣服实际赚了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com