练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形ABCD的边长为3cm，∠ABE=，且AB=AE，则DE的长度为（ ）

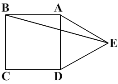
    A. 3 B. 4 C. 5 D. 6

    【答案】A

    【解析】

    根据∠ABE=15°，AB=AE，易得∠AEB=∠ABE=15°，再根据AD∥BC，可得∠EBC=75°，∠AFE=105°，∠DAE=60°，进而可得ADE=∠AED=60°，故△ADE是等边三角形，由等边三角形的性质可得DE的长．

    如图：AD交BE于点F,∵∠ABE=15°，AB=AE

    ∴∠AEB=∠ABE=15°

    ∴∠EFD=∠AFB=90°15°=75°

    故∠AFE=180°75°=105°

    ∴∠DAE=180°105°15°=60°

    又∵AB=AE

    ∴△ADE是等边三角形，

    所以DE=AD=3cm.

    故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直线L上有三个正方形a，b，c，若a，c的面积分别为1和9，则b的面积为（ ）

    A．8 B．9 C．10 D．11

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】十一黄金周期间，某景点门票价格为：成人票每张80元，儿童票每张20元，甲旅行团有x名成人和y名儿童；乙旅行团的成人数是甲旅行团的2倍，儿童数是甲旅行团的．

    （1）甲、乙两个旅行团在该景点的门票费用分别为：甲　 　元；乙　 　元；（用含x、y的代数式表示）

    （2）若x＝10，y＝6，求两个旅行团门票费用的总和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市公交公司为应对春运期间的人流高峰，计划购买A、B两种型号的公交车共10辆，若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车3辆，共需650万元，

    （1）试问该公交公司计划购买A型和B型公交车每辆各需多少万元？

    （2）若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元，且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次，则该公司有哪几种购车方案？哪种购车方案的总费用W最少？最少总费用是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，AF是⊙O切线，CD是垂直于AB的弦，垂足为E，过点C作DA的平行线与AF相交于点F，CD=，BE=2．

    求证：（1）四边形FADC是菱形；

    （2）FC是⊙O的切线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题学习】小芸在小组学习时问小娟这样一个问题：已知α为锐角，且sin α＝，求sin 2α的值．

    小娟是这样给小芸讲解的：

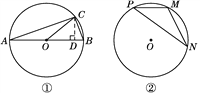
    如图①，在⊙O中，AB是直径，点C在⊙O上，所以∠ACB＝90°. 设∠BAC＝α，则sin α＝＝.易得∠BOC＝2α.设BC＝x，则AB＝3x，AC＝2 x.作CD⊥AB于D，求出CD＝________(用含x的式子表示)，可求得sin 2α＝＝________.

    【问题解决】已知，如图②，点M，N，P为⊙O上的三点，且∠P＝β，sin β＝，求sin 2β的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

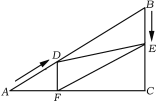
    【题目】如图，在Rt△ABC中，∠C=90°，AB=60cm，∠A=30°，点D从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，同时点E从点B出发沿BC方向以1cm/秒的速度向点C匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤30）．过点D作DF⊥AC于点F，连接DE，EF．

    （1）填空：四边形BEFD是_________；

    （2）当t=______时，四边形BEFD能够成为菱形。

    （3）当t为何值时？△DEF为直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：

    为解方程（x2﹣1）2﹣5（x2﹣1）+4=0，我们可以将x2﹣1视为一个整体，然后设x2﹣1=y，则原方程化为y2﹣5y+4=0，解此方程得：y1=1，y2=4．

    当y=1时，x2﹣1═1，∴x=±．

    当y=4时，x2﹣1═4，∴x=±．

    ∴原方程的解为：x1=，x2=﹣，x3=，x4=﹣．

    以上方法叫做换元法解方程，达到了降次的目的，体现了转化思想．

    运用上述方法解方程：x4﹣8x2+12=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

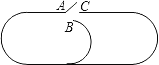
    【题目】如图是一个玩具火车轨道，A点有个变轨开关，可以连接B或C．小圈轨道的周长是1.5米，大圈轨道的周长是3米．开始时，A连接C，火车从A点出发，按照顺时针方向再轨道上移动，同时变轨开关每隔一分钟变换一次轨道连接．若火车的速度是每分钟10米，则火车第10次回到A点时用了______分钟．

    查看答案和解析>>

    同步练习册答案