
【题目】如图,直线L上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为( )

A.8 B.9 C.10 D.11
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣6)﹣(+15)+4﹣(﹣15)
(2)﹣2×3﹣(﹣4)×2+3
(3)(![]() ﹣
﹣![]()
![]() )×(﹣24)
)×(﹣24)
(4)﹣14﹣2×(﹣3)2÷(﹣![]() )
)
(5)﹣18÷(﹣3)2+5×(﹣2)3﹣(﹣15)÷5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间定价增加10x元(x为整数).
(1)直接写出每天游客居住的房间数量y与x的函数关系式;
(2)设宾馆每天的利润为w元,当每间房价定价为多少元时,宾馆每天所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
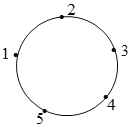
【题目】圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2020次“移位”后,他到达编号为______的点.
查看答案和解析>>
科目:初中数学 来源: 题型:
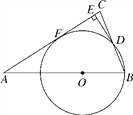
【题目】如图,在△ABC中,AB=AC,O在AB上,以O为圆心,OB长为半径的圆与BC交于点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相切于F,AB=5,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月25日,中国国际大数据产业博览会在贵阳会展中心开幕,博览会设了编号为1~6号展厅共6个,小雨一家计划利用两天时间参观其中两个展厅:第一天从6个展厅中随机选择一个,第二天从余下的5个展厅中再随机选择一个,且每个展厅被选中的机会均等.
(1)第一天,1号展厅没有被选中的概率是 ;
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com