
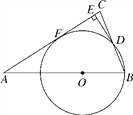
【题目】如图,在△ABC中,AB=AC,O在AB上,以O为圆心,OB长为半径的圆与BC交于点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相切于F,AB=5,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OD,由OB=OD,AB=AC,可得到∠ODB=∠C,即OD∥AC,而DE⊥AC,即可得到OD⊥DE,从而得到DE是⊙O的切线.
(2)根据切线的性质定理,连接过切点的半径,运用锐角三角函数的定义,用半径表示OA的长,再根据AB的长列方程求解.
(1)证明:连接OD,∵OB=OD,∴∠ABC=∠ODB.∵AB=AC,∴∠ABC=∠ACB,(2分)∴∠ODB=∠ACB,∴OD∥AC.∵DE⊥AC,∴OD⊥DE,∴DE是⊙O的切线.
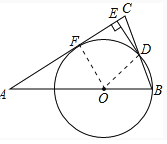
(2)解:连接OF,则OF⊥AC.∵在Rt△OAF中,sinA=![]() =
=![]() ,∴OA=
,∴OA=![]() OF.又∵AB=OA+OB=5,∴
OF.又∵AB=OA+OB=5,∴![]() OF+OF=5,∴OF=
OF+OF=5,∴OF=![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若a2=16,|b|=3,且ab<0,求a+b的值;
(2)已知a、b互为相反数且a≠0,c、d互为倒数,m的绝对值是5,求m2﹣(﹣1)+![]() (a+b)﹣cd的值.
(a+b)﹣cd的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,他这天下午行驶里程如下:(单位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他将最后一名乘客送到目的地时,距下午出车地点是多少千米?
(2)若汽车耗油量为![]() 升∕千米,这天下午共耗油多少升
升∕千米,这天下午共耗油多少升
查看答案和解析>>
科目:初中数学 来源: 题型:
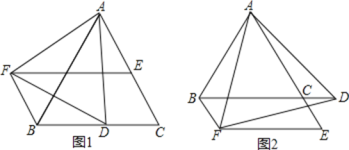
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并回答问题.我们知道|a|的几何意义是指数轴上表示数的点与原点的距离,那么|a-b|的几何意义又是什么呢?我们不妨考虑一下,取特殊值时的情况.比如考虑|5-(-6)|的几何意义,在数轴上分别标出表示-6和5的点,(如图所示),两点间的距离是11,而|5-(-6)|=11,因此不难看出|5-(-6)|就是数轴上表示-6和5两点间的距离.
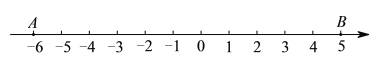
(1)|a-b|的几何意义是_______;
(2)当|x-2|=2时,求出x的值.
(3)设Q=|x+6|-|x-5|,请问Q是否存在最大值,若没有请说明理由,若有,请求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,AB=6,AD=8,将矩形ABCD绕点A顺时针旋转θ(0°<θ<360°)得到矩形AEFG,当θ=_____°时,GC=GB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sin α=![]() ,求sin 2α的值.
,求sin 2α的值.
小娟是这样给小芸讲解的:
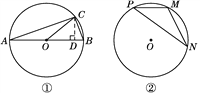
如图①,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°. 设∠BAC=α,则sin α=![]() =
=![]() .易得∠BOC=2α.设BC=x,则AB=3x,AC=2
.易得∠BOC=2α.设BC=x,则AB=3x,AC=2![]() x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=
x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=![]() =________.
=________.
【问题解决】已知,如图②,点M,N,P为⊙O上的三点,且∠P=β,sin β=![]() ,求sin 2β的值.
,求sin 2β的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com