
【题目】如图,点A是反比例函数y=![]() (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.

【答案】(1) B(2n,![]() );(2)证明见解析;(3)y=x+6.
);(2)证明见解析;(3)y=x+6.
【解析】
试题(1)由题意可表示出点A的坐标,根据BD是AC的中垂线可得点B的纵坐标,代入反比例函数解析式即可求得横坐标;
(2)先根据AM=CM、BM=MD证明四边形ABCD是平行四边形,再根据BD⊥AC即可证明四边形ABCD是菱形;
(3)根据题意求得点A、B的坐标即可得.
试题解析:(1)当x=n时,y=![]() ,∴A(n,
,∴A(n,![]() ),
),
由题意知BD是AC的中垂线,∴点B的纵坐标为![]() ,
,
∴把y=![]() 代入y=
代入y=![]() 得x=2n,∴B(2n,
得x=2n,∴B(2n,![]() );
);
(2)由(1)可知AM=CM,BM=MD=![]() ,
,
∴四边形ABCD是平行四边形,
又∵BD⊥AC,∴平行四边形ABCD是菱形;
(3)当四边形ABCD是正方形时,△ABM为等腰直角三角形,
∵△ABM的面积为2,∴AM=BM=2,∴A(-2,4),B(-4,2),
由此可得直线AB所对应的函数表达式为y=x+6.


科目:初中数学 来源: 题型:
【题目】如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE与BF相交于O.下列结论:①AE=BF;②AE⊥BF;③AO=OE;④![]() .其中正确的有( )
.其中正确的有( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的日历表,在此目历表上可以用一个“十”字圈出5个数.
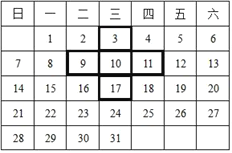
(1)如图中四周的4个数3、9、17、11的和与中间的数10有什么数量关系?
(2)照此方法,任意圈出的5个数是否都具有这样的数量关系?请通过整式的运算说明理由.
(3)用(2)的结论说明圈出的5个数的和能否等于125?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个菱形的两个顶点与一个正方形的两个顶点重合,并且这两个四边形没有公共边,菱形的面积为24cm2,正方形的面积为32cm2,则菱形的边长为______________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k≠0)与一次函数y=-x+5的一个交点是A(1,n).
(k≠0)与一次函数y=-x+5的一个交点是A(1,n).
(1)求反比例函数y=![]() (k≠0)的表达式;
(k≠0)的表达式;
(2)当一次函数的函数值大于反比例函数的函数值时,直接写出自变量x的取值范围为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国高铁近年来用震惊世界的速度不断发展,已成为当代中国一张耀眼的“国家名片”。修建高铁时常常要逢山开道、遇水搭桥。如图,某高铁在修建时需打通一直线隧道MN(M、N为山的两侧),工程人员为了计算MN两点之间的直线距离,选择了在测量点A、B、C进行测量,点B、C分别在AM、AN上,现测得AM=1200米,AN=2000米,AB=30米,BC=45米,AC=18米,求直线隧道MN的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-12017+(π-3)0+(-![]() )
)
(2)(-a)3a2+(2a4)2÷a3
(3) 6 (-x2-xy+y2)(-xy)
(4) x2-(x+2) (x-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
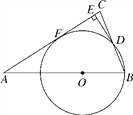
【题目】如图,在△ABC中,AB=AC,O在AB上,以O为圆心,OB长为半径的圆与BC交于点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相切于F,AB=5,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com