Question

【题目】已知一个菱形的两个顶点与一个正方形的两个顶点重合，并且这两个四边形没有公共边，菱形的面积为24cm2，正方形的面积为32cm2，则菱形的边长为______________cm.

Answer 1

【答案】

【解析】

①如图1，由正方形ABCD的面积为32cm2，得到BC=4cm，求得EF=6，连接EF交BC于O，根据勾股定理得到菱形的边长为cm；②如图2，由正方形ABCD的面积为32cm2，得到BD=8cm，求得EF=6，连接EF交BC于O，根据勾股定理得到菱形的边长为5cm．③AC或BD为边的菱形，也满足条件，

解：①如图1，

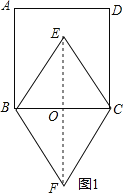
∵正方形ABCD的面积为32cm2，

∴BC=4cm，

∵菱形EBFC面积为24cm2，

∴EFBC=24，

∴EF=6，

连接EF交BC于O，

∴EF⊥BC，BO=CO=BC=2，OE=EF=3，

∴,，

∴菱形的边长为cm；

②如图2，∵正方形ABCD的面积为32cm2，

∴BD=8cm，

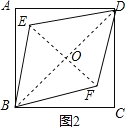
∵菱形EBFC面积为24cm2，

∴EFBC=24，

∴EF=6，

连接EF交BC于O，

∴EF⊥BC，BO=CO=BD=4，OE=EF=3

∴=5，

∴菱形的边长为5cm；

③AC或BD为边的菱形，也满足条件．

综上所述，菱形的边长为或5或8．