【题目】如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根．

（1）求C点坐标；

（2）求直线MN的解析式；

（3）在直线MN上存在点P，使以点P，B，C三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．

参考答案：

【答案】（1）C（0，6）。

（2）y=x+6。

（3）P1（4，3），P2（）P3（），P4（）。

【解析】

试题

（1）通过解方程x2﹣14x+48=0可以求得OC=6，OA=8．则C（0，6）；

（2）设直线MN的解析式是y=kx+b（k≠0）．把点A、C的坐标分别代入解析式，列出关于系数k、b的方程组，通过解方程组即可求得它们的值；

（3）需要分类讨论：PB为腰，PB为底两种情况下的点P的坐标．根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答．

试题解析：

（1）解方程x2-14x+48=0得

x1=6，x2=8

∵OA，OC（OA＞OC）的长分别是一元二次方程x2-14x+48=0的两个实数根

∴OC=6，OA=8

∴C（0，6）

（2）设直线MN的解析式是y=kx+b（k≠0）

由（1）知，OA=8，则A（8，0）

∵点A、C都在直线MN上

∴

解得，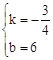

∴直线MN的解析式为y=-x+6

（3）

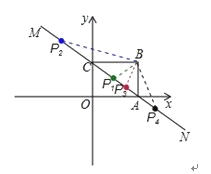
∵A（8，0），C（0，6）

∴根据题意知B（8，6）

∵点P在直线MN y=-x+6上

∴设P（a，--a+6）

当以点P，B，C三点为顶点的三角形是等腰三角形时，需要分类讨论：

①当PC=PB时，点P是线段BC的中垂线与直线MN的交点，则P1（4，3）；

②当PC=BC时，a2+（-a+6-6）2=64

解得，a=±，则P2（-，），P3（，）

③当PB=BC时，（a-8）2+（-a+6-6）2=64

解得，a=，则-a+6=-

∴P4（，）

综上所述，符合条件的点P有：P1（4，3），P2(-，)，P3(，)，P4（，-）

关闭