
ЁОЬтФПЁПШчЭМЃЌОЙ§ЕуAЃЈ0ЃЌЉ4ЃЉЕФХзЮяЯпy= ![]() x2+bx+cгыxжсЯрНЛгкЕуBЃЈЉ1ЃЌ0ЃЉКЭCЃЌOЮЊзјБъдЕуЃЎ
x2+bx+cгыxжсЯрНЛгкЕуBЃЈЉ1ЃЌ0ЃЉКЭCЃЌOЮЊзјБъдЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉНЋХзЮяЯпy= ![]() x2+bx+cЯђЩЯЦНвЦ
x2+bx+cЯђЩЯЦНвЦ ![]() ИіЕЅЮЛГЄЖШЃЌдйЯђзѓЦНвЦmЃЈmЃО0ЃЉИіЕЅЮЛГЄЖШЃЌЕУЕНаТХзЮяЯпЃЌШєаТХзЮяЯпЕФЖЅЕуPдкЁїABCФкЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ИіЕЅЮЛГЄЖШЃЌдйЯђзѓЦНвЦmЃЈmЃО0ЃЉИіЕЅЮЛГЄЖШЃЌЕУЕНаТХзЮяЯпЃЌШєаТХзЮяЯпЕФЖЅЕуPдкЁїABCФкЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉНЋxжсЯТЗНЕФХзЮяЯпЭМЯѓЙигкxжсЖдГЦЃЌЕУЕНаТЕФКЏЪ§ЭМЯѓCЃЌШєжБЯпy=x+kгыЭМЯѓCЪМжега3ИіНЛЕуЃЌЧѓТњзуЬѕМўЕФkЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКЁпОЙ§ЕуAЃЈ0ЃЌЉ4ЃЉЕФХзЮяЯпy= ![]() x2+bx+cгыxжсЯрНЛгкЕуBЃЈЉ1ЃЌ0ЃЉЃЌ
x2+bx+cгыxжсЯрНЛгкЕуBЃЈЉ1ЃЌ0ЃЉЃЌ
Ёр  ЃЌ
ЃЌ
Ёр  ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊy= ![]() x2Љ
x2Љ ![]() xЉ4
xЉ4
ЃЈ2ЃЉ
НтЃКгЩЃЈ1ЃЉжЊЃЌХзЮяЯпНтЮіЪНЮЊy= ![]() x2Љ
x2Љ ![]() xЉ4=
xЉ4= ![]() ЃЈx2Љ7xЃЉЉ4=
ЃЈx2Љ7xЃЉЉ4= ![]() ЃЈxЉ
ЃЈxЉ ![]() ЃЉ2Љ
ЃЉ2Љ ![]() ЃЌ
ЃЌ
ЁрДЫХзЮяЯпЯђЩЯЦНвЦ ![]() ИіЕЅЮЛГЄЖШЕФХзЮяЯпЕФНтЮіЪНЮЊy=
ИіЕЅЮЛГЄЖШЕФХзЮяЯпЕФНтЮіЪНЮЊy= ![]() ЃЈxЉ
ЃЈxЉ ![]() ЃЉ2Љ
ЃЉ2Љ ![]() ЃЌ
ЃЌ
дйЯђзѓЦНвЦmЃЈmЃО0ЃЉИіЕЅЮЛГЄЖШЃЌЕУЕНаТХзЮяЯпy= ![]() ЃЈx+mЉ
ЃЈx+mЉ ![]() ЃЉ2Љ
ЃЉ2Љ ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФЖЅЕуPЃЈЉm+ ![]() ЃЌЉ
ЃЌЉ ![]() ЃЉЃЌ
ЃЉЃЌ
ЖдгкХзЮяЯпy= ![]() x2Љ
x2Љ ![]() xЉ4ЃЌСюy=0ЃЌ
xЉ4ЃЌСюy=0ЃЌ ![]() x2Љ
x2Љ ![]() xЉ4=0ЃЌНтЕУx=Љ1Лђ8ЃЌ
xЉ4=0ЃЌНтЕУx=Љ1Лђ8ЃЌ
ЁрBЃЈ8ЃЌ0ЃЉЃЌЁпAЃЈ0ЃЌЉ4ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊy=Љ4xЉ4ЃЌжБЯпACЕФНтЮіЪНЮЊy= ![]() xЉ4ЃЌ
xЉ4ЃЌ
ЕБЖЅЕуPдкABЩЯЪБЃЌЉ ![]() =Љ4ЁСЃЈЉm+
=Љ4ЁСЃЈЉm+ ![]() ЃЉЉ4ЃЌНтЕУm=
ЃЉЉ4ЃЌНтЕУm= ![]() ЃЌ
ЃЌ
ЕБЖЅЕуPдкACЩЯЪБЃЌЉ ![]() =
= ![]() ЃЈЉm+
ЃЈЉm+ ![]() ЃЉЉ4ЃЌНтЕУm=
ЃЉЉ4ЃЌНтЕУm= ![]() ЃЌ
ЃЌ
ЁрЕБЕуPдкЁїABCФкЪБ ![]() ЃМmЃМ
ЃМmЃМ ![]()
ЃЈ3ЃЉ
НтЃКЗелКѓЫљЕУаТЭМЯѓШчЭМЫљЪОЃЎ

ЦНвЦжБЯпy=x+kжЊЃКжБЯпЮЛгкl1КЭl2ЪБЃЌЫќгыаТЭМЯѓгаШ§ИіВЛЭЌЕФЙЋЙВЕуЃЎ
ЂйЕБжБЯпЮЛгкl1ЪБЃЌДЫЪБl1Й§ЕуBЃЈЉ1ЃЌ0ЃЉЃЌ
Ёр0=Љ1+kЃЌМДk=1ЃЎ
ЂкЁпЕБжБЯпЮЛгкl2ЪБЃЌДЫЪБl2гыКЏЪ§y=Љ ![]() x2+
x2+ ![]() x+4ЃЈЉ1ЁмxЁм8ЃЉЕФЭМЯѓгавЛИіЙЋЙВЕу
x+4ЃЈЉ1ЁмxЁм8ЃЉЕФЭМЯѓгавЛИіЙЋЙВЕу
ЁрЗНГЬx+k=Љ ![]() x2+
x2+ ![]() x+4ЃЌМДx2Љ5xЉ8+2k=0гаСНИіЯрЕШЪЕИљЃЎ
x+4ЃЌМДx2Љ5xЉ8+2k=0гаСНИіЯрЕШЪЕИљЃЎ
ЁрЁї=25Љ4ЃЈ2kЉ8ЃЉ=0ЃЌМДk= ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌkЕФжЕЮЊ1Лђ ![]()
ЁОНтЮіЁПЃЈ1ЃЉИУХзЮяЯпЕФНтЮіЪНжажЛгаСНИіД§ЖЈЯЕЪ§ЃЌжЛашНЋAЁЂBСНЕузјБъДњШыМДПЩЕУНтЃЎЃЈ2ЃЉЪзЯШИљОнЦНвЦЬѕМўБэЪОГівЦЖЏКѓЕФКЏЪ§НтЮіЪНЃЌНјЖјгУmБэЪОГіИУКЏЪ§ЕФЖЅЕузјБъЃЌНЋЦфДњШыжБЯпABЁЂACЕФНтЮіЪНжаЃЌМДПЩШЗЖЈPдкЁїABCФкЪБmЕФШЁжЕЗЖЮЇЃЎЃЈ3ЃЉЯШИљОнКЏЪ§НтЮіЪНЛГіЭМаЮЃЌШЛКѓНсКЯЭМаЮевГіХзЮяЯпгыxжсгаШ§ИіНЛЕуЕФЧщаЮЃЌзюКѓЧѓЕУжБЯпЕФНтЮіЪНЃЌДгЖјПЩЧѓЕУmЕФжЕЃЎ
ЁОПМЕуОЋЮіЁПеЦЮеЖўДЮКЏЪ§ЕФЭМЯѓКЭЖўДЮКЏЪ§ЕФаджЪЪЧНтД№БОЬтЕФИљБОЃЌашвЊжЊЕРЖўДЮКЏЪ§ЭМЯёЙиМќЕуЃК1ЁЂПЊПкЗНЯђ2ЁЂЖдГЦжс 3ЁЂЖЅЕу 4ЁЂгыxжсНЛЕу 5ЁЂгыyжсНЛЕуЃЛдіМѕадЃКЕБa>0ЪБЃЌЖдГЦжсзѓБпЃЌyЫцxдіДѓЖјМѕаЁЃЛЖдГЦжсгвБпЃЌyЫцxдіДѓЖјдіДѓЃЛЕБa<0ЪБЃЌЖдГЦжсзѓБпЃЌyЫцxдіДѓЖјдіДѓЃЛЖдГЦжсгвБпЃЌyЫцxдіДѓЖјМѕаЁЃЎ


 НнОЖбЕСЗМьВтОэЯЕСаД№АИ
НнОЖбЕСЗМьВтОэЯЕСаД№АИ аЁЗђзгШЋФмМьВтЯЕСаД№АИ
аЁЗђзгШЋФмМьВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпЕФВЛЕШЪНЮЊy=Љx2+6x+cЃЎ
ЃЈ1ЃЉШєХзЮяЯпгыxжсгаНЛЕуЃЌЧѓcЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЩшХзЮяЯпгыxжсСНИіНЛЕуЕФКсзјБъЗжБ№ЮЊx1 ЃЌ x2 ЃЎ Шєx12+x22=26ЃЌЧѓcЕФжЕЃЎ
ЃЈ3ЃЉШєPЃЌQЪЧХзЮяЯпЩЯЮЛгкЕквЛЯѓЯоЕФВЛЭЌСНЕуЃЌPAЃЌQBЖМДЙжБгкxжсЃЌДЙзуЗжБ№ЮЊAЃЌBЃЌЧвЁїOPAгыЁїOQBШЋЕШЃЎЧѓжЄЃКcЃОЉ ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
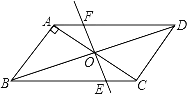
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDжаЃЌABЁЭACЃЌAB=1ЃЌBC=![]() ЃЎЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌНЋжБЯпACШЦЕуOЫГЪБеыа§зЊЃЌЗжБ№НЛBCЃЌADгкЕуEЃЌFЃЎ
ЃЎЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌНЋжБЯпACШЦЕуOЫГЪБеыа§зЊЃЌЗжБ№НЛBCЃЌADгкЕуEЃЌFЃЎ
ЃЈ1ЃЉжЄУїЃКЕБа§зЊНЧЮЊ90ЁуЪБЃЌЫФБпаЮABEFЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉЪдЫЕУїдка§зЊЙ§ГЬжаЃЌЯпЖЮAFгыECзмБЃГжЯрЕШЃЛ
ЃЈ3ЃЉдка§зЊЙ§ГЬжаЃЌЫФБпаЮBEDFПЩФмЪЧСтаЮТ№ЃПШчЙћВЛФмЃЌЧыЫЕУїРэгЩЃЛШчЙћФмЃЌЫЕУїРэгЩВЂЧѓГіДЫЪБACШЦЕуOЫГЪБеыа§зЊЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЁїABCжаЃЌAB:BC:CA=3:4:5ЃЌЧвжмГЄЮЊ36cmЃЌЕуPДгЕуAПЊЪМбиABБпЯђЕуBвдУПУы1cmЕФЫйЖШвЦЖЏЃЛЕуQДгЕуBбиBCБпЯђЕуCвдУПУы2cmЕФЫйЖШвЦЖЏЃЛШчЙћЭЌЪБГіЗЂЃЌдђЙ§3УыЪБЃЌЧѓЁїBPQЕФУцЛ§ЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуPЃЈmЃЌnЃЉдкЕквЛЯѓЯоЃЌЧвдкжБЯпy=-x+6ЩЯЃЌЕуAЕФзјБъЮЊЃЈ5,0ЃЉЃЌOЪЧзјБъдЕуЃЌЁїPAOЕФУцЛ§ЪЧS.
ЃЈ1ЃЉЧѓSгыmЕФКЏЪ§ЙиЯЕЪНЃЌВЂЛГіКЏЪ§SЕФЭМЯѓЃЛ
ЃЈ2ЃЉаЁНмШЯЮЊЁїPAOЕФУцЛ§ПЩвдЮЊ15ЃЌФуШЯЮЊФиЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§y=x2+bxЭМЯѓЕФЖдГЦжсЮЊжБЯпx=1ЃЌШєЙигкxЕФвЛдЊЖўДЮЗНГЬx2+bxЉt=0ЃЈtЮЊЪЕЪ§ЃЉдкЉ1ЁмxЁм3ЕФЗЖЮЇФкгаНтЃЌдђtЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпMNгыxжсЃЌyжсЗжБ№ЯрНЛгкAЃЌCСНЕуЃЌЗжБ№Й§AЃЌCСНЕузїxжсЃЌyжсЕФДЙЯпЯрНЛгкBЕуЃЌЧвOAЃЌOCЃЈOAЃОOCЃЉЕФГЄЗжБ№ЪЧвЛдЊЖўДЮЗНГЬx2Љ14x+48=0ЕФСНИіЪЕЪ§ИљЃЎ

ЃЈ1ЃЉЧѓCЕузјБъЃЛ
ЃЈ2ЃЉЧѓжБЯпMNЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкжБЯпMNЩЯДцдкЕуPЃЌЪЙвдЕуPЃЌBЃЌCШ§ЕуЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧыжБНгаДГіPЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкЦНааЫФБпаЮABCDжаЃЌAB=6ЃЌBC=10ЃЌЁЯBAD=120ЁуЃЌEЮЊЯпЖЮBCЩЯЕФвЛИіЖЏЕуЃЈВЛгыBЃЌCжиКЯЃЉЃЌЙ§EзїжБЯпABЕФДЙЯпЃЌДЙзуЮЊFЃЌFEгыDCЕФбгГЄЯпЯрНЛгкЕуGЃЌ
ЃЈ1ЃЉШчЭМ1ЃЌЕБAEЁЭBCЪБЃЌЧѓЯпЖЮBEЁЂCGЕФГЄЖШЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕуEдкЯпЖЮBCЩЯдЫЖЏЪБЃЌСЌНгDEЃЌDFЃЌЁїBEFгыЁїCEGЕФжмГЄжЎКЭЪЧЗёЪЧвЛИіЖЈжЕЃЌШєЪЧЧыЧѓГіЖЈжЕЃЌШєВЛЪЧЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌЩшBE=xЃЌЁїDEFЕФУцЛ§ЮЊyЃЌЪдЧѓГіyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com