
【题目】某汽车租赁公司要购买轿车和面包车共![]() 辆.其中面包车不能超过轿车的两倍,轿车每辆
辆.其中面包车不能超过轿车的两倍,轿车每辆![]() 万元,面包车每辆
万元,面包车每辆![]() 万元,公司可投入的购车款不超过61万元.
万元,公司可投入的购车款不超过61万元.
(小题1)符合公司要求的购买方案有哪几种?请说明理由.
(小题2)如果每辆轿车的日租金为![]() 元,每辆面包车的日租金为
元,每辆面包车的日租金为![]() 元.假设新购买的这
元.假设新购买的这![]() 辆车每日都可租出,要使这
辆车每日都可租出,要使这![]() 辆车的日租金收入不低于1600元,那么应选择以上哪种购买方案?
辆车的日租金收入不低于1600元,那么应选择以上哪种购买方案?
【答案】【1】符合公司要求的购买方案有四种,理由见详解;
【2】要使这10辆车的日租金收入不低于1600元,那么应选择面包车购买3辆,轿车购买7辆或选择面包车购买4辆,轿车购买6辆.
【解析】
(1)设面包车购买x辆,根据某汽车租赁公司要购买轿车和面包车共10辆.其中面包车不能超过轿车的两倍,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过61万元可列不等式求解.
(2)根据求出的方案,可依次求出每种方案的租金,求出符合要求的方案.
(1)设面包车购买x辆,依题意得:
![]()
解这个不等式组得:3![]() x
x![]()
根据题意,x应为正整数,∴x=3、4、5、6;
当x=3,10x=7;
当x=4,10x=6;
当x=5,10x=5;
当x=6,10x=4;
答:符合公司要求的购买方案有四种.
(2)方案一租金收入:110×3+200×7=1730(元)
方案二日租金收入:110×4+200×6=1640(元)
方案三日租金收入:110×5+200×5=1550(元)
方案四日租金收入:110×6+200×4=1460(元)
答:要使这10辆车的日租金收入不低于1600元,那么应选择面包车购买3辆,轿车购买7辆或选择面包车购买4辆,轿车购买6辆.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】计算
(1) (1-1![]() -
-![]() +
+![]() )×(-24)
)×(-24)
(2) 1![]() ×
×![]() -(-
-(-![]() )×2
)×2![]() +(-
+(-![]() )+
)+![]()
(3)(-119![]() )×5
)×5
(4)(![]() )÷(
)÷(![]() )2÷|-
)2÷|-![]() |+(-1)4+(0.25)2003×42003
|+(-1)4+(0.25)2003×42003
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个菱形的两个顶点与一个正方形的两个顶点重合,并且这两个四边形没有公共边,菱形的面积为24cm2,正方形的面积为32cm2,则菱形的边长为______________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k≠0)与一次函数y=-x+5的一个交点是A(1,n).
(k≠0)与一次函数y=-x+5的一个交点是A(1,n).
(1)求反比例函数y=![]() (k≠0)的表达式;
(k≠0)的表达式;
(2)当一次函数的函数值大于反比例函数的函数值时,直接写出自变量x的取值范围为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国高铁近年来用震惊世界的速度不断发展,已成为当代中国一张耀眼的“国家名片”。修建高铁时常常要逢山开道、遇水搭桥。如图,某高铁在修建时需打通一直线隧道MN(M、N为山的两侧),工程人员为了计算MN两点之间的直线距离,选择了在测量点A、B、C进行测量,点B、C分别在AM、AN上,现测得AM=1200米,AN=2000米,AB=30米,BC=45米,AC=18米,求直线隧道MN的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
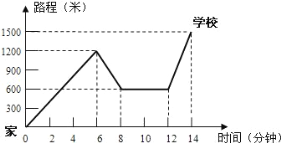
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-12017+(π-3)0+(-![]() )
)
(2)(-a)3a2+(2a4)2÷a3
(3) 6 (-x2-xy+y2)(-xy)
(4) x2-(x+2) (x-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在的直线折叠得到△AFE,延长AF交CD于点G,已知CG=2,DG=1,则BC的长是( )

A.3![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com