
【题目】中国高铁近年来用震惊世界的速度不断发展,已成为当代中国一张耀眼的“国家名片”。修建高铁时常常要逢山开道、遇水搭桥。如图,某高铁在修建时需打通一直线隧道MN(M、N为山的两侧),工程人员为了计算MN两点之间的直线距离,选择了在测量点A、B、C进行测量,点B、C分别在AM、AN上,现测得AM=1200米,AN=2000米,AB=30米,BC=45米,AC=18米,求直线隧道MN的长。

科目:初中数学 来源: 题型:
【题目】如图,已知A(3,1)与B(1,0),PQ是直线![]() 上的一条动线段且
上的一条动线段且![]() (Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )
(Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )

A.(![]() ,
,![]() )B.(
)B.(![]() ,
,![]() )C.(0,0)D.(1,1)
)C.(0,0)D.(1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P(1,﹣4)、Q(m,n)在函数![]() (x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )

A.减小 B.增大 C.先减小后增大 D.先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,对角线AC.BD相交于点O,下列结论不一定正确的是( )

A.AC=BDB.OB=OCC.∠BCD=∠BDCD.∠ABD=∠ACD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司要购买轿车和面包车共![]() 辆.其中面包车不能超过轿车的两倍,轿车每辆
辆.其中面包车不能超过轿车的两倍,轿车每辆![]() 万元,面包车每辆
万元,面包车每辆![]() 万元,公司可投入的购车款不超过61万元.
万元,公司可投入的购车款不超过61万元.
(小题1)符合公司要求的购买方案有哪几种?请说明理由.
(小题2)如果每辆轿车的日租金为![]() 元,每辆面包车的日租金为
元,每辆面包车的日租金为![]() 元.假设新购买的这
元.假设新购买的这![]() 辆车每日都可租出,要使这
辆车每日都可租出,要使这![]() 辆车的日租金收入不低于1600元,那么应选择以上哪种购买方案?
辆车的日租金收入不低于1600元,那么应选择以上哪种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若a2=16,|b|=3,且ab<0,求a+b的值;
(2)已知a、b互为相反数且a≠0,c、d互为倒数,m的绝对值是5,求m2﹣(﹣1)+![]() (a+b)﹣cd的值.
(a+b)﹣cd的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并回答问题.我们知道|a|的几何意义是指数轴上表示数的点与原点的距离,那么|a-b|的几何意义又是什么呢?我们不妨考虑一下,取特殊值时的情况.比如考虑|5-(-6)|的几何意义,在数轴上分别标出表示-6和5的点,(如图所示),两点间的距离是11,而|5-(-6)|=11,因此不难看出|5-(-6)|就是数轴上表示-6和5两点间的距离.
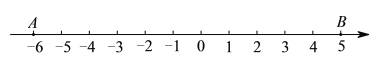
(1)|a-b|的几何意义是_______;
(2)当|x-2|=2时,求出x的值.
(3)设Q=|x+6|-|x-5|,请问Q是否存在最大值,若没有请说明理由,若有,请求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com